Z testa formula statistikā Soli pa solim aprēķins (piemēri)

Z testa aprēķināšanas formula statistikā

Z Tests statistikā attiecas uz hipotēzes testu, ko izmanto, lai noteiktu, vai abi aprēķinātie vidējie parametri ir atšķirīgi, ja ir pieejamas standarta novirzes un ja izlase ir liela.

Z = (x - μ) / ơ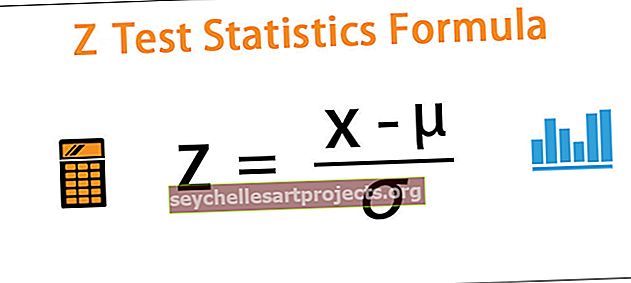

kur x = jebkura vērtība no populācijas

μ = populācijas vidējais lielums
population = populācijas standartnovirze

Parauga gadījumā vērtības z-testa statistikas formulu aprēķina, no x vērtības atņemot vidējo paraugu un pēc tam rezultātu dalot ar parauga standartnovirzi. Matemātiski tas tiek attēlots kā

Z = (x - x_nozīmē ) / s

kur

x = jebkura vērtība no izlases
x_mean = vidējais paraugs
s = parauga standartnovirze

Z testa aprēķins (soli pa solim)

Z-testa statistikas formula populācijai tiek iegūta, veicot šādas darbības:

1. solis: Pirmkārt, aprēķiniet populācijas vidējo vērtību un populācijas standartnovirzi, pamatojoties uz novērojumu, kas iegūts populācijas vidējā vērtībā, un katru novērojumu apzīmē ar x _i . Kopējo novērojumu skaitu populācijā apzīmē ar N.

Vidējais iedzīvotāju skaits,

Populācijas standartnovirze,

2. solis: Visbeidzot, z-testa statistiku aprēķina, no mainīgā atņemot iedzīvotāju vidējo lielumu, un pēc tam rezultāts tiek dalīts ar populācijas standartnovirzi, kā parādīts zemāk.

Z = (x - μ) / ơ

Formula z-testa statistikai paraugam tiek iegūta, veicot šādas darbības:

1. solis: Pirmkārt, aprēķiniet parauga vidējo lielumu un parauga standartnovirzi tāpat kā iepriekš. Šeit kopējais novērojumu skaits izlasē tiek apzīmēts ar n tā, ka n <N.

Vidējais paraugs,

Standarta novirzes paraugs,

2. solis: Visbeidzot, z-testa statistiku aprēķina, no x vērtības atņemot vidējo paraugu, un pēc tam rezultātu dala ar parauga standartnovirzi, kā parādīts zemāk.

Z = (x - x_nozīmē ) / s

Piemēri

Šo Z testa formulas Excel veidni varat lejupielādēt šeit - Z testa formulas Excel veidne

1. piemērs

Pieņemsim, ka skolā ir tādu skolēnu skaits, kuri ieradās klases pārbaudījumam. Vidējais rezultāts testā ir 75, un standartnovirze ir 15. Nosakiet Deivida z-testa rezultātu, kurš testā ieguva 90 punktus.

Ņemot vērā

Vidējais iedzīvotāju skaits, μ = 75
Iedzīvotāju standartnovirze, ơ = 15

Tāpēc z testa statistiku var aprēķināt kā

Z = (90 - 75) / 15

Z Testa statistika būs -

Z = 1

Tāpēc Dāvida testa rezultāts ir viena standarta novirze virs vidējā iedzīvotāju skaita, ti, saskaņā ar z-punktu tabulu 84,13% studentu ir mazāk vērtējuši nekā Deivids.

2. piemērs

Ņemsim piemēru no 30 studentiem, kuri tika izvēlēti kā daļa no apsekojamās izlases komandas, lai redzētu, cik zīmuļu tika lietoti nedēļā. Nosakiet z-testa rezultātu 3. studentam, pamatojoties uz dotajām atbildēm: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Ņemot vērā

x = 5, kopš 3. studenta atbildes, ir 5
Parauga lielums, n = 30

Vidējais paraugs = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Vidējais = 4,17

Tagad parauga standartnovirzi var aprēķināt, izmantojot iepriekš minēto formulu.

ơ = 1,90

Tāpēc z-testa rezultātu 3. studentam var aprēķināt kā:

Z = (x - x) / s

Z = (5 –17) / 1,90
Z = 0,44

Tāpēc 3. studenta lietojums ir 0,44 reizes lielāks par standarta novirzi virs vidējā parauga izmantojuma, ti, kā norādīts z-punktu tabulā, 67% studentu lieto mazāk zīmuļu nekā 3. students.

3. piemērs

Zemāk ir sniegti dati Z testa statistikas aprēķināšanai

Lai iegūtu detalizētu Z testa statistikas aprēķinu, varat atsaukties uz norādīto Excel lapu.

Atbilstība un lietojumi

Ir ļoti svarīgi izprast z-testa statistikas jēdzienu, jo to parasti lieto vienmēr, kad ir strīdīgi, vai testa statistika atbilst normālam sadalījumam attiecīgajā nulles hipotēzē. Tomēr jāpatur prātā, ka z-tests tiek izmantots tikai tad, ja parauga lielums ir lielāks par 30, pretējā gadījumā tiek izmantots t-tests.

seychellesartprojects.org