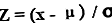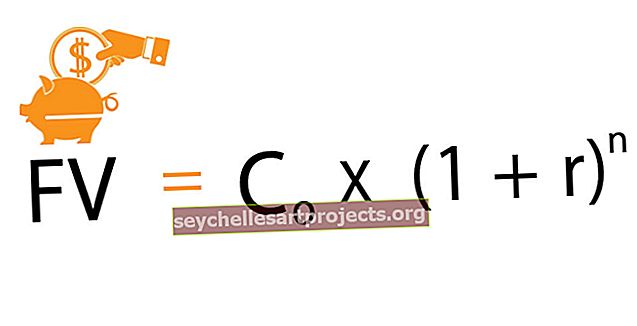seychellesartprojects.org

Z-rādītāja aprēķināšanas formula

Neapstrādātu datu Z-rādītājs attiecas uz rezultātu, kas iegūts, mērot, cik daudz standarta noviržu ir virs vai zem populācijas vidējā, ir dati, kas palīdz pārbaudīt izskatāmo hipotēzi. Citiem vārdiem sakot, datu punkta attālums no vidējā vidējā lieluma tiek izteikts kā standarta novirzes reizinājums.

• Z rādītāji svārstās diapazonā no -3 reizes lielāks par standarta novirzi (normālā sadalījuma tālu kreisajā pusē) līdz +3 reizes lielāks par standarta novirzi (normālā sadalījuma labajā pusē pa labi).
• Z rādītāju vidējais rādītājs ir 0 un standartnovirze 1.

Datu punkta z-rādītāja vienādojumu aprēķina, no datu punkta atņemot vidējo populācijas vidējo vērtību (turpmāk - x ), un pēc tam rezultātu dala ar populācijas standartnovirzi. Matemātiski tas tiek attēlots kā

Z rādītājs = (x - μ) / ơ

kur

• x = Datapunkt
• μ = vidējais
• ơ = standartnovirze

Z rādītāja aprēķināšana (soli pa solim)

Datu punkta z-score vienādojumu var iegūt, izmantojot šādas darbības:

• 1. solis: Pirmkārt, nosakiet datu kopas vidējo vērtību, pamatojoties uz datu punktiem vai novērojumiem, kas apzīmēti ar x _i , bet kopējais datu punktu skaits datu kopā ir apzīmēts ar N.

• 2. solis: Pēc tam nosakiet populācijas standartnovirzi, pamatojoties uz populācijas vidējo μ, datu punktiem x _i un datu punktu skaitu populācijā N.

• 3. solis: Visbeidzot, z-punktu iegūst, vidējo vērtību atņemot no datu punkta, un pēc tam rezultātu dala ar standarta novirzi, kā parādīts zemāk.

  

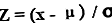
Piemēri

Šo Z Score Formula Excel veidni varat lejupielādēt šeit - Z Score Formula Excel veidne

1. piemērs

Ņemsim piemēru no 50 studentu klases, kas pagājušajā nedēļā ir uzrakstījuši dabaszinātņu pārbaudījumu. Šodien ir rezultātu diena, un klases audzinātāja pastāstīja, ka Jānis testā ieguva 93 punktus, savukārt klases vidējais vērtējums bija 68. Nosakiet Jāņa testa zīmes z punktu skaitu, ja standartnovirze ir 13.

Risinājums:

Ņemot vērā

• Jāņa testa rezultāts, x = 93
• Vidējais, μ = 68
• Standarta novirze, ơ = 13

Tāpēc Jāņa testa rezultāta z-punktu var aprēķināt, izmantojot iepriekš minēto formulu,

Z = (93 - 68) / 13

Z rādītājs būs -

Z rādītājs = 1,92

Tāpēc Jāņa Ztest rādītājs ir 1,92 standartnovirze virs klases vidējā rādītāja, kas nozīmē, ka 97,26% klases (49 skolēni) rādītāji bija mazāki nekā Džonam.

2. piemērs

Ņemsim vēl vienu detalizētu piemēru ar 30 skolēniem (jo z-tests nav piemērots mazāk nekā 30 datu punktiem), kuri ieradās klases pārbaudījumam. Nosakiet z-testa rezultātu 4. studentam, pamatojoties uz studentu atzīmēm no 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 , 65, 52, 54, 83., 86., 94., 85., 72., 62., 64., 74., 82., 58., 57., 51., 91. lpp.

Risinājums:

Ņemot vērā

• x = 65,
• 4. students atzīmēja = 65,
• Datu punktu skaits, N = 30.

Vidējais = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30

Vidējais = 71.30

Tagad standartnovirzi var aprēķināt, izmantojot formulu, kā parādīts zemāk,

ơ = 13,44

Tāpēc 4. studenta Z-punktu var aprēķināt, izmantojot iepriekš minēto formulu,

Z = (x - x) / s

• Z = (65 –30) / 13,44
• Z = -0,47

Tāpēc 4. studenta rezultāts ir 0,47 standartnovirze zem klases vidējā rezultāta, kas nozīmē, ka 31,92% klases (10 skolēni) vērtējums bija mazāks nekā 4. studentam, kā norādīts z-punktu tabulā.

Z rādītājs programmā Excel (ar Excel veidni)

Tagad izmantosim 2. piemērā minēto gadījumu, lai ilustrētu z-score jēdzienu zemāk esošajā Excel veidnē.

Zemāk ir sniegti dati Z rādītāja aprēķināšanai

Lai iegūtu detalizētu Z rādītāja formulas testa statistikas aprēķinu, varat atsaukties uz norādīto Excel lapu.

Atbilstība un lietojumi

No hipotēzes pārbaudes viedokļa z-score ir ļoti svarīgs jēdziens, kas jāsaprot, jo to izmanto, lai pārbaudītu, vai testa statistika ietilpst pieņemamajā vērtību diapazonā. Z-score tiek izmantots arī, lai standartizētu datus pirms analīzes, aprēķinātu rezultātu varbūtību vai salīdzinātu divus vai vairākus datu punktus, kas ir no dažādiem normāliem sadalījumiem. Pareizi lietojot z-score, laukos var izmantot daudzveidīgi.