seychellesartprojects.org

Histogrammas diagrammas piemēri

Histogramma attiecas uz vizuālo noformējumu, ko izmanto, lai apkopotu diskrētos vai nepārtrauktos datus, un kura piemērs ietver vizuālo noformējumu diagrammā, klienta sūdzības, kas veiktas bankā par dažādiem parametriem, kur būs visvairāk reģistrētais sūdzības iemesls ir augstākais attēlā redzamajā diagrammā.

Ja dažāda augstuma joslas tiek izmantotas datu parādīšanai grafiskā formā, to sauc par histogrammas diagrammu. Katra josla histogrammā tiek grupēta diapazonos. Joslas, kuru izmērs ir augstāks, parāda, ka lielākā daļa datu ietilpst šajā augstākajā diapazonā. Histogramma attēlo nepārtrauktās dotās datu kopas vai doto paraugu izplatību un formu. Šajā rakstā mēs sniegsim 4 galvenos histogrammas diagrammu piemērus.

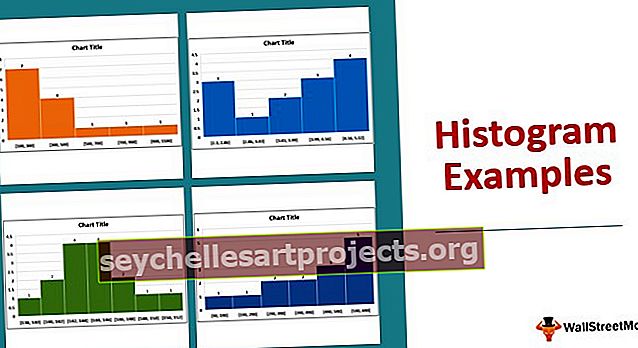
4 galvenie histogrammas diagrammu piemēri

Zemāk ir 4 galvenie histogrammas diagrammu piemēri.

Histogrammas 1. piemērs

SBI vadītājs Šovs kungs ir noraizējies par klientu sūdzībām par garām rindām filiālē. Viņš vispirms vēlas analizēt, cik bieži notiek galvenā klienta gaidīšanas laiks. Viņš ir izsaucis kasieri un lūdzis viņam detaļas.

Zemāk ir norādīts klienta gaidīšanas laiks SBI bankas filiāles kasē pīķa stundās, ko novēroja kasieris. Jums ir jāizveido histogramma, pamatojoties uz tālāk norādītajiem datiem.

Risinājums:

Mēs esam izveidojuši histogrammu, izmantojot 5 tvertnes ar 5 dažādām frekvencēm, kā redzams zemāk diagrammā. Y asī tas ir vidējais klientu skaits, kas ietilpst šajā konkrētajā kategorijā. X asī mums ir gaidīšanas laika diapazons, piemēram, 1. atkritumu tvertnes diapazons ir no 2,30 minūtēm līdz 2,86 minūtēm. Un mēs varam atzīmēt, ka tabulā šai kategorijai ir 3 skaitļi un kā redzams zemāk redzamajā diagrammā.

Tas ir nejaušs sadalījums, kas ir sadalījuma veids, kuram ir vairākas virsotnes, un tam trūkst acīmredzama modeļa.

Var būt scenārijs, kurā tika apvienoti dažādi datu rekvizīti. Tādējādi dati būtu jāanalizē atsevišķi.

Histogrammas piemērs # 2

Mr Larry slavens ārsts veic pētījumus par studentu augumu, kas mācās 8. standartā. Viņš ir apkopojis 15 studentu izlasi, bet vēlas uzzināt, kura maksimālā kategorija ir vieta, kur viņi pieder.

Risinājums:

 Mēs esam izveidojuši histogrammu, izmantojot 6 tvertnes ar 6 dažādām frekvencēm, kā redzams zemāk diagrammā. Y asī tas ir vidējais studentu skaits, kas nokrīt šajā kategorijā. X asī mums ir augstuma diapazons, piemēram, 1. atkritumu tvertnes diapazons ir no 138 cm līdz 140 cm. Un mēs varam atzīmēt, ka tabulā šai kategorijai ir 1 skaitlis un kā redzams zemāk redzamajā diagrammā.

Šeit mēs varam redzēt studentu augstumu vidēji diapazonā no 142 cm līdz 146 cm 8. standartam. Un arī var atzīmēt, ka viena vidējā puse krīt arī vidējā otrā pusē, kas ir normāla sadalījuma zīme.

Histogrammas 3. piemērs

A kungs vēlas veikt ieguldījumu akciju tirgū. Viņš ir iekļāvis zemāk par akcijām un vēlas uzzināt cenu biežumu.

Izmantojiet histogrammu un norādiet, kāda veida sadalījums tas ir?

Risinājums:

Mēs esam izveidojuši histogrammu, izmantojot 5 tvertnes ar 5 dažādām frekvencēm, kā redzams zemāk diagrammā. Y asī tas ir konkrētajā kategorijā ietilpstošo krājumu skaits. X asī mums ir akciju cenu diapazons, piemēram, 1. atkritumu tvertnes diapazons ir no 100 līdz 300. Un mēs varam atzīmēt, ka tabulā šīs kategorijas skaits ir 7 un kā redzams zemāk redzamajā diagrammā.

Šeit mēs varam atzīmēt, ka grafiks ir novirzīts uz kreiso pusi, un līdz ar to tas ir sadalījuma pazīme, kas ir sadalīta pa labi. Liels skaits datu vērtību parādās kreisajā pusē un mazāk datu labajā pusē.

Histogrammas 4. piemērs

Indijas kriketa komandas treneris Šastri veic sikspārņu vidējā rezultāta analīzi un vēlas pabeigt izvēlētos sikspārņus gaidāmajam pasaules kausam. Tomēr viņš vispirms ir ieinteresēts izveidot etalonu, lai izvēlētos sikspārņus. Viņš ir saņēmis zemāk esošo sikspārņu sarakstu viņu pēdējās 15 maiņās, taču vēlas uzzināt, kāds ir dīvainais no šī saraksta. Izmantojiet histogrammu, atrodiet to un komentējiet izplatīšanu.

Risinājums:

Mēs esam izveidojuši histogrammu, izmantojot 6 tvertnes ar 6 dažādām frekvencēm, kā redzams zemāk diagrammā. Y asī tas ir sikspārņu skaits, kas ietilpst šajā konkrētajā kategorijā. X asī mums ir darbības diapazons, piemēram, 1. atkritumu tvertnes diapazons ir no 90 līdz 190. Un mēs varam atzīmēt, ka tabulā šai kategorijai ir 1 skaitlis un kā redzams zemāk redzamajā diagrammā.

Mēs varam redzēt, ka augstāk esošajā tabulā parādīts šķērsvirziena sadalījums pa kreisi. Labajā pusē ir liels skaits datu, bet kreisajā pusē - mazāks skaits datu.

90 skrējieni 15 maiņās, šķiet, ir nepāra, un šķiet, ka ir bļodiņa, un tāpēc tie ir jānoņem.

Secinājums

Izveidojot histogrammu, tiks iegūts attēlojums, kas ir vizuāls pēc dotās datu kopas vai datu izplatīšanas. Histogrammas parāda datu vērtību biežumu un lielu datu daudzumu. Histogramma palīdz noteikt mediānu un dotās datu kopas sadalījumu. Turklāt tas var parādīt visas nepilnības vai visus novirzes dotajā datu kopā.