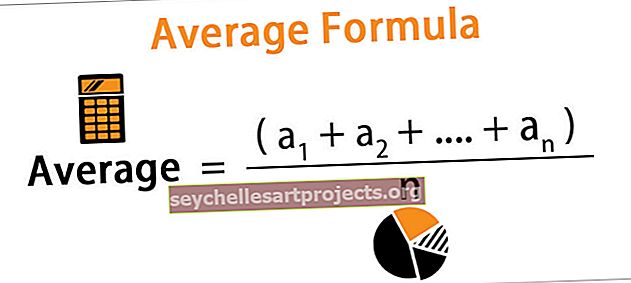Ģeometriskais vidējais vs vidējais aritmētiskais 9 galvenās atšķirības (ar infografiku)
Atšķirības starp vidējo ģeometrisko un aritmētisko
Ģeometriskais vidējais ir produkta vērtību sērijas vidējā vai vidējā līmeņa aprēķins, kurā ņemta vērā salikšanas ietekme, un to izmanto, lai noteiktu ieguldījumu veiktspēju, bet vidējais aritmētiskais ir vidējā aprēķins ar vērtību kopsummas dalījumu ar skaitli vērtību.

Ģeometrisko vidējo vērtību aprēķina skaitļu sērijai, ņemot šo skaitļu reizinājumu un paaugstinot to līdz sērijas apgrieztajam garumam, turpretim vidējais aritmētiskais ir vienkārši vidējais un tiek aprēķināts, saskaitot visus skaitļus un dalot ar šīs sērijas skaitu no skaitļiem.
Ģeometriskā vidējā vs vidējā aritmētiskā infografika

Galvenās atšķirības
- Aritmētiskais vidējais ir pazīstams kā vidējais aritmētiskais un tiek izmantots ikdienas atgriešanas aprēķinos. Ģeometriskais vidējais ir pazīstams kā multiplikatīvais vidējais, un tas ir maz sarežģīts un ietver salikšanu
- Galvenā atšķirība abos šajos vidējos veidos ir tā aprēķināšanas veids. Aritmētisko vidējo vērtību aprēķina kā visu skaitļu summu, kas dalīta ar datu kopas numuru. Ģeometriskais vidējais ir skaitļu sērija, kas aprēķināta, ņemot šo skaitļu reizinājumu un paaugstinot to līdz sērijas garuma apgrieztajai vērtībai
- Ģeometriskā vidējā formula ir {[(1 + Return1) x (1 + Return2) x (1 + Return3) ...)] ^ (1 / n)]} - 1 un aritmētiskajam vidējam ir (Return1 + Return2 + Return3 + Return4 ) / 4.
- Ģeometrisko vidējo var aprēķināt tikai pozitīviem skaitļiem, un tas vienmēr ir mazāks par ģeometrisko, tikmēr aritmētisko vidējo var aprēķināt gan pozitīvajiem, gan negatīvajiem skaitļiem, un tas vienmēr ir lielāks par ģeometrisko vidējo
- Visizplatītākā datu kopas problēma ir izslēgto vērtību ietekme. 11, 13, 17 un 1000 datu kopā ģeometriskais vidējais ir 39,5, bet vidējais aritmētiskais ir 260,75. Efekts ir skaidri izcelts. Ģeometriskais vidējais normalizē datu kopu, un vērtības tiek aprēķinātas kā vidējās, tādējādi svaros nedominē neviens diapazons, un jebkuram procentam nav būtiskas ietekmes uz datu kopu. Ģeometrisko vidējo neietekmē šķībie sadalījumi, kā tas ir aritmētiskajā vidējā vērtībā.
- Statistikas speciālisti izmanto vidējo aritmētisko, bet datu kopai bez būtiskiem izņēmumiem. Šāda veida vidējā vērtība ir noderīga temperatūras nolasīšanai. Tas ir noderīgi arī automašīnas vidējā ātruma noteikšanā. No otras puses, ģeometriskais vidējais ir noderīgs gadījumos, kad datu kopa ir logaritmiska vai mainās ar 10 reizinājumiem.
- Daudzi biologi izmanto šāda veida vidējo līmeni, lai aprakstītu baktēriju populācijas lielumu. Piemēram, baktēriju populācija var būt 10 vienā dienā un 10 000 citās. Ienākumu sadalījumu var aprēķināt arī, izmantojot ģeometrisko vidējo. Piemēram, X un Y gadā nopelna 30 000 USD, bet Z - 300 000 USD gadā. Šajā gadījumā vidējais aritmētiskais nebūs noderīgs. Portfeļa pārvaldnieki uzsver, kā indivīda labklājība un par to ir palielinājusies vai samazinājusies.
Salīdzinošā tabula
| Pamats | Ģeometriskais vidējais | Aritmētiskais vidējais | ||
| Nozīme | Ģeometriskais vidējais ir pazīstams kā multiplikatīvais vidējais | Aritmētiskais vidējais ir zināms kā piedevas vidējais | ||
| Formula | {[(1 + Return1) x (1 + Return2) x (1 + Return3)…)] ^ (1 / n)]} - 1 | (Return1 + Return2 + Return3 + Return4) / 4 | ||
| Vērtības | Ģeometriskais vidējais vienmēr ir zemāks par vidējo aritmētisko savienojuma efekta dēļ | Aritmētiskais vidējais lielums vienmēr ir lielāks par vidējo ģeometrisko, jo to aprēķina kā vienkāršu vidējo | ||
| Aprēķins | Pieņemsim, ka datu kopai ir šādi skaitļi - 50, 75, 100. Ģeometrisko vidējo vērtību aprēķina kā kuba sakni no (50 x 75 x 100) = 72,1 | Līdzīgi datu kopai ar 50, 75 un 100 vidējo aritmētisko vērtību aprēķina kā (50 + 75 + 100) / 3 = 75 | ||
| Datu kopa | Tas ir piemērojams tikai pozitīvam skaitļu kopumam | To var aprēķināt gan ar pozitīvu, gan negatīvu skaitļu kopu | ||
| Lietderība | Ģeometriskais vidējais var būt noderīgāks, ja datu kopa ir logaritmiska. Atšķirība starp abām vērtībām ir garums | Šī metode ir piemērotāka, aprēķinot neatkarīgu notikumu kopas rezultātu vidējo vērtību | ||
| Outlier efekta ietekme | Ārkārtas ietekme uz ģeometrisko vidējo ir viegla. Apsveriet datu kopu 11,13,17 un 1000. Šajā gadījumā 1000 ir ārpusrādītājs. Šeit vidējais rādītājs ir 39,5 | Aritmētiskajam vidējam rādītājam ir nopietna ietekme uz ārējiem rādītājiem. 11,13,17 un 1000 datu kopā vidējais rādītājs ir 260,25 | ||
| Izmanto | Ģeometrisko vidējo vērtību izmanto biologi, ekonomisti, kā arī galvenokārt finanšu analītiķi. Tas ir vispiemērotākais datu kopai, kurai ir korelācija | Aritmētisko vidējo izmanto, lai attēlotu vidējo temperatūru, kā arī automašīnas ātrumu |
Secinājums
Ģeometriskā vidējā izmantošana ir piemērota procentuālajām izmaiņām, svārstīgajiem skaitļiem un datiem, kuriem ir korelācija, īpaši ieguldījumu portfeļiem. Lielākā daļa finanšu ienesīguma ir savstarpēji saistītas, piemēram, akcijas, obligāciju ienesīgums un prēmijas. Ilgāks periods padara salikšanas efektu svarīgāku un līdz ar to arī ģeometriskā vidējā izmantošanu. Lai gan neatkarīgām datu kopām piemērotāks ir aritmētiskais, jo tas ir vienkārši lietojams un viegli saprotams.