Ilguma formula (definīcija, Excel piemēri) Aprēķiniet obligācijas ilgumu
Kas ir ilguma formula?
Ilguma formula ir obligācijas jutīguma rādītājs pret procentu likmes izmaiņām, un to aprēķina, dalot obligācijas nākotnes naudas ieplūdes diskontēto summu un atbilstošo gadu skaitu ar diskontētās nākotnes naudas ieplūdes summu. Naudas plūsmu galvenokārt veido kupona maksājums un termiņš beigās. To sauc arī par Makolija ilgumu.
Matemātiski ilguma vienādojums ir attēlots zemāk,

kur,
- C = kupona maksājums par periodu
- M = sejas vai nominālvērtība
- r = efektīvā periodiskā procentu likme
- n = termiņu termiņu skaits
Turklāt saucējs, kas ir obligācijas diskontētās naudas ieplūdes summa, ir ekvivalents obligācijas pašreizējai vērtībai vai cenai. Tāpēc ilguma formulu var vēl vairāk vienkāršot, kā norādīts zemāk,

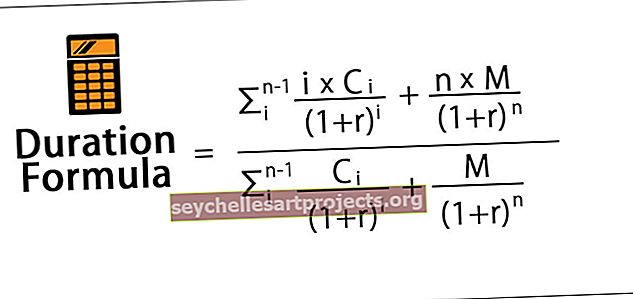
Ilguma formulas skaidrojums
Ilguma vienādojumu var aprēķināt, veicot šādas darbības:
1. solis: Pirmkārt, tiek aprēķināta obligāciju emisijas nominālvērtība vai nominālvērtība, un to apzīmē ar M.
2. solis: Tagad obligācijas kupona maksājums tiek aprēķināts, pamatojoties uz procentu faktisko periodisko likmi. Tad tiek noteikts arī kupona maksājuma biežums. Kupona maksājumu apzīmē ar C, un faktisko periodisko procentu likmi apzīmē ar r.
3. solis: Tagad kopējais periodu skaits līdz termiņa beigām tiek aprēķināts, reizinot gadu skaitu līdz termiņam un kupona maksājumu biežumu gadā. Periodu skaitu līdz termiņa beigām apzīmē ar n. Tiek atzīmēts arī periodiskā maksājuma laiks, ko apzīmē ar i.
4. solis: Visbeidzot, pamatojoties uz pieejamo informāciju, ilguma vienādojumu var iegūt šādi:

Ilguma formulas piemēri (ar Excel veidni)
Apskatīsim dažus vienkāršus un uzlabotus ilguma formulas veidus, lai to labāk saprastu.
Šo Duration Formula Excel veidni varat lejupielādēt šeit - Duration Formula Excel veidne
Ilgums Formula Formula - 1. piemērs
Ņemsim piemēru obligācijai ar gada kupona maksājumiem. Pieņemsim, ka uzņēmums XYZ Ltd ir izlaidis obligācijas, kuras nominālvērtība ir 100 000 USD, ar gada kupona likmi 7% un kuras dzēšanas termiņš ir 5 gadi. Dominējošā tirgus procentu likme ir 10% .
Ņemot vērā, M = 100 000 USD
- C = 7% * 100 000 USD = 7 000 USD
- n = 5
- r = 10%
Saucēju vai obligācijas cenu aprēķina, izmantojot šādu formulu:

- Obligāciju cena = 84,281,19
Formulas Ilgums skaitītāja aprēķins ir šāds:

= (6 363,64 + 11 570,25 + 15 777,61 + 19 124,38 + 310 460,70)
= 363,296,50
Tāpēc obligācijas ilgums tiks aprēķināts šādi:

Ilgums = 363 296,50 / 84 281,19
- Ilgums = 4,31 gads
Ilgums Formula Formula - 2. piemērs
Ņemsim piemēru obligācijai ar gada kupona maksājumiem. Pieņemsim, ka uzņēmums XYZ Ltd ir izlaidis obligācijas, kuras nominālvērtība ir 100 000 USD un kuras dzēšanas termiņš ir 4 gadi. Dominējošā tirgus procentu likme ir 10%. Aprēķiniet obligāciju ilgumu šādai gada kupona likmei: (a) 8% (b) 6% (c) 4%
Ņemot vērā, M = 100 000 USD
- n = 4
- r = 10%
Aprēķins par kupona likmi 8%
Kupona maksājums (C) = 8% * 100 000 USD = 8 000 USD
Saucēju vai obligācijas cenu aprēķina, izmantojot šādu formulu:

- Obligāciju cena = 88 196,16
Formulas Duration skaitītāja aprēķins būs šāds:

= 311 732,8
Tāpēc obligācijas ilgums tiks aprēķināts šādi:

Ilgums = 311 732,81 / 88 196,16
- Ilgums = 3,53 gadi
Aprēķins par kuponu likmi 6%
Kupona maksājums (C) = 6% * 100 000 USD = 6000 USD
Saucēju vai obligācijas cenu aprēķina, izmantojot šādu formulu:

- Obligāciju cena = 83 222,46
Formulas Duration skaitītāja aprēķins būs šāds:

= 302,100,95
Tāpēc obligācijas ilgums tiks aprēķināts šādi:

Ilgums = 302 100,95 / 83 222,46
- Ilgums = 63 gadi
Aprēķins par kupona likmi 4%
Kupona maksājums = 4% * 100 000 USD = 4 000 USD
Saucēju vai obligācijas cenu aprēķina, izmantojot šādu formulu:

- Obligāciju cena = 78 248,75
Formulas Duration skaitītāja aprēķins būs šāds:

= 292 469,09
Tāpēc obligācijas ilgums tiks aprēķināts šādi:

Ilgums Formula = 292 469,09 / 78 248,75
- Ilgums = 3,74 gadi
No piemēra redzams, ka obligācijas ilgums palielinās, samazinoties kupona likmei.
Ilguma formulas atbilstība un izmantošana
Ir svarīgi saprast ilguma jēdzienu, jo obligāciju ieguldītāji to izmanto, lai pārbaudītu obligācijas jutīgumu pret procentu likmju izmaiņām. Obligācijas ilgums būtībā norāda, cik daudz obligāciju tirgus cena mainīsies procentu likmes izmaiņu dēļ. Jāatceras, ka procentu likme un obligāciju cena virzās pretējos virzienos un kā obligāciju cena pieaug, kad procentu likme samazinās, un otrādi.
Gadījumā, ja investori vēlas gūt labumu no procentu likmes krituma, ieguldītāji plāno iegādāties ilgāka termiņa obligācijas, kas ir iespējams obligācijām ar zemāku kupona maksājumu un ilgu dzēšanas termiņu. No otras puses, ieguldītājiem, kuri vēlas izvairīties no procentu likmju svārstībām, ieguldītājiem būs jāiegulda obligācijās, kurām ir mazāks termiņš vai īss termiņš un augstāks kupona maksājums.