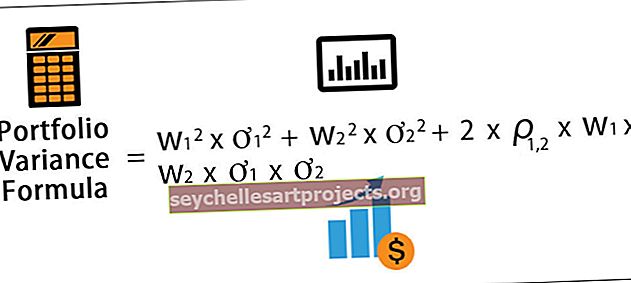Portfeļa dispersijas formula (piemērs) | Kā aprēķināt portfeļa dispersiju?
Kas ir portfeļa dispersija?
Termins “portfeļa dispersija” attiecas uz mūsdienu ieguldījumu teorijas statistisko vērtību, kas palīdz noteikt portfeļa vidējās atdeves izkliedi no tā vidējā. Īsāk sakot, tas nosaka kopējo portfeļa risku. To var iegūt, pamatojoties uz vidējo svērto individuālo dispersiju un savstarpējo kovariāciju.
Portfeļa dispersijas formula
Matemātiski portfeļa dispersijas formula, kas sastāv no diviem aktīviem, tiek attēlota kā
Portfeļa dispersijas formula = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2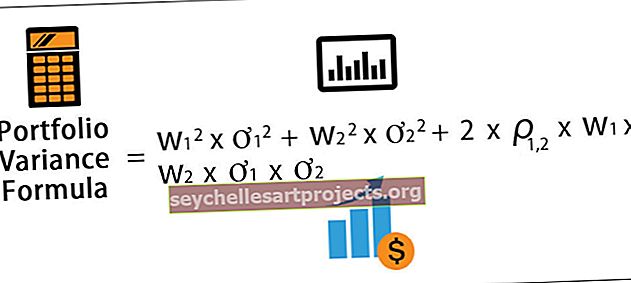
kur,
- w i = aktīva i portfeļa svars
- ơ i 2 = Aktīva i individuālā dispersija
- ρ i, j = korelācija starp aktīvu i un aktīvu j
Atkal, dispersiju var vēl paplašināt, iekļaujot portfelī vairāk nē. aktīvu, piemēram, 3 aktīvu portfeli var attēlot kā
Portfeļa dispersijas formula = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Portfeļa dispersijas formulas skaidrojums
Konkrēta portfeļa portfeļa dispersijas formulu var iegūt, veicot šādas darbības:
1. solis: Pirmkārt, nosakiet katra aktīva svaru kopējā portfelī, un to aprēķina, dalot aktīvu vērtību ar kopējo portfeļa vērtību. I-tā aktīva svars tiek apzīmēts ar w i .
2. solis: Pēc tam nosakiet katra aktīva standartnovirzi, un tā tiek aprēķināta, pamatojoties uz katra aktīva vidējo un faktisko atdevi. I-tā aktīva standartnovirzi apzīmē ar ơ i . Standartnovirzes kvadrāts ir dispersija, ti, ơ i 2.
3. solis: Pēc tam nosakiet korelāciju starp aktīviem, un tā pamatā atspoguļo katra aktīva kustību attiecībā pret citu aktīvu. Korelāciju apzīmē ar ρ.
4. solis: Visbeidzot, divu aktīvu portfeļa dispersijas formula tiek iegūta, pamatojoties uz individuālās dispersijas un savstarpējās kovariances vidējo svērto vērtību, kā parādīts zemāk.
Portfeļa dispersijas formula = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Portfeļa varianta formulas piemērs (ar Excel veidni)
Šo Portfolio Variance Formula Excel veidni varat lejupielādēt šeit - Portfolio Variance Formula Excel Template
Ņemsim piemēru no portfeļa, kas sastāv no divām akcijām. A krājuma vērtība ir 60 000 USD un tā standartnovirze ir 15%, savukārt B akcijas vērtība ir 90 000 USD un tā standartnovirze ir 10%. Starp abiem krājumiem pastāv korelācija 0,85. Nosakiet dispersiju.
Ņemot vērā
- Krājuma A standartnovirze, ơ A = 15%
- B krājuma standartnovirze, ơ B = 10%
Korelācija, ρ A, B = 0,85
Zemāk ir dati divu akciju portfeļa dispersijas aprēķināšanai.

Akcijas A svars, w A = 60 000 USD / (60 000 USD + 90 000 USD) * 100%

Akcijas A svars = 40% vai 0,40
B krājuma svars, w B = 90 000 USD / (60 000 USD + 90 000 USD) * 100%

Akcijas B svars = 60% vai 0,60
Tāpēc portfeļa dispersijas aprēķins būs šāds,

Dispersija = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Tāpēc dispersija ir 1,33%.
Atbilstība un izmantošana
Viena no spilgtākajām portfeļa var pazīmēm ir fakts, ka tā vērtību iegūst, pamatojoties uz katra aktīva individuālo dispersiju svērto vidējo svērto vērtību, kas koriģētas pēc to kovariācijām. Tas norāda, ka kopējā novirze ir mazāka nekā katra portfeļa akcijas atsevišķo svārstību vienkāršā svērtā vidējā vērtība. Jāatzīmē, ka portfelim ar vērtspapīriem, kuru savstarpējā korelācija ir mazāka, galu galā ir mazāka portfeļa dispersija.
Svarīga ir arī izpratne par portfeļa dispersijas formulu, jo tā tiek izmantota mūsdienu portfeļa teorijā, kas balstīta uz pamata pieņēmumu, ka normāli investori plāno maksimāli palielināt savu atdevi, vienlaikus samazinot risku, piemēram, dispersiju. Investors parasti veic tā saukto efektīvo robežu, un tas ir zemākais riska vai svārstīguma līmenis, ar kuru ieguldītājs var sasniegt savu mērķa atdevi. Visbiežāk investori iegulda nekorelētos aktīvos, lai mazinātu risku saskaņā ar Mūsdienu portfeļa teoriju.
Ir gadījumi, kad aktīvi, kas individuāli varētu būt riskanti, galu galā var mazināt portfeļa dispersiju, jo šāds ieguldījums, visticamāk, pieaugs, kad kritīsies citi ieguldījumi. Šī samazinātā korelācija kā tāda var palīdzēt samazināt hipotētiskā portfeļa dispersiju. Parasti portfeļa riska līmeni mēra, izmantojot standartnovirzi, kuru aprēķina kā dispersijas kvadrātsakni. Paredzams, ka dispersija saglabāsies augsta, ja datu punkti ir tālu no vidējā, kas galu galā rada arī augstāku kopējo riska līmeni portfelī.