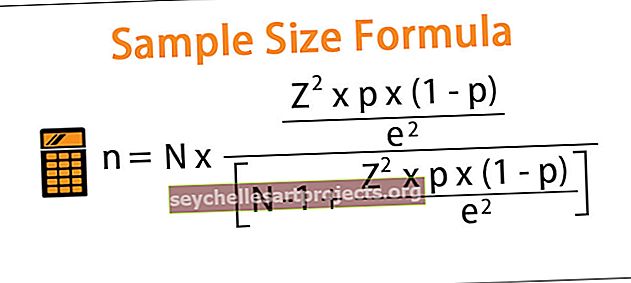seychellesartprojects.org

Formula, lai noteiktu populācijas izlases lielumu

Izlases lieluma formula palīdz aprēķināt vai noteikt minimālo izlases lielumu, kas nepieciešams, lai uzzinātu adekvātu vai pareizu kopas daļu, kā arī ticamības līmeni un kļūdu robežu.

Termins “izlase” attiecas uz to iedzīvotāju daļu, kas ļauj mums izdarīt secinājumus par populāciju, tāpēc ir svarīgi, lai izlases lielums būtu pietiekami piemērots, lai varētu izdarīt nozīmīgus secinājumus. Citiem vārdiem sakot, tas ir minimālais lielums, kas nepieciešams, lai novērtētu patieso populācijas proporciju ar nepieciešamo kļūdu robežu un ticamības līmeni. Piemērotas izlases lieluma noteikšana ir viena no statistikas analīzes atkārtotajām problēmām. Tās vienādojumu var iegūt, izmantojot populācijas lielumu, normālā sadalījuma kritisko vērtību, izlases proporciju un kļūdas robežu.

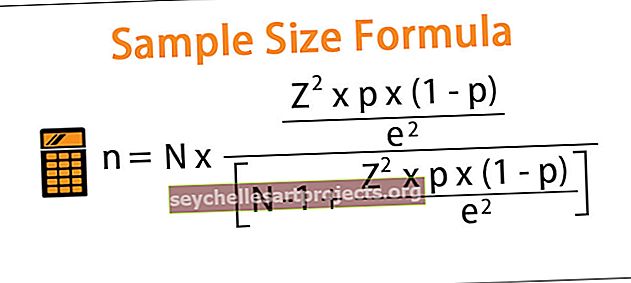
kur,

• N = populācijas lielums,
• Z = normālā sadalījuma kritiskā vērtība pie vajadzīgā ticamības līmeņa,
• p = parauga daļa,
• e = kļūdas robeža

Kā aprēķināt parauga lielumu? (Soli pa solim)

• 1. solis: Pirmkārt, nosakiet populācijas lielumu, kas ir kopējais atsevišķo vienību skaits jūsu populācijā, un to apzīmē ar N. [Piezīme: Gadījumā, ja populācijas lielums ir ļoti liels, bet precīzs skaits nav zināms, tad izmantojiet 100 000 jo izlases lielums daudz nemainās lielākām populācijām.]
• 2. solis: Pēc tam nosakiet normālā sadalījuma kritisko vērtību vajadzīgajā ticamības līmenī. Piemēram, kritiskā vērtība 95% ticamības līmenī ir 1,96.
• 3. solis: Pēc tam nosakiet izlases daļu, kuru var izmantot pēc iepriekšējiem apsekojuma rezultātiem vai kuru var savākt, veicot nelielu izmēģinājuma aptauju. [Piezīme: ja neesat pārliecināts, ka vienmēr var izmantot 0,5 kā konservatīvu pieeju, un tas dos pēc iespējas lielāku izlases lielumu.]
• 4. solis: Pēc tam nosakiet kļūdas robežu, kas ir diapazons, kurā paredzams, ka patiesā populācija atrodas . [Piezīme: mazāka kļūdas robeža, jo lielāka ir precizitāte un līdz ar to arī precīza atbilde.]
• 5. solis: Visbeidzot, izlases lieluma vienādojumu var iegūt, izmantojot populācijas lielumu (1. solis), normālā sadalījuma kritisko vērtību vajadzīgajā ticamības līmenī (2. solis), izlases proporciju (3. solis) un kļūdas robežu (solis). 4) kā parādīts zemāk.

Piemēri

Šo parauga lieluma formulas Excel veidni varat lejupielādēt šeit - parauga lieluma formulas Excel veidne

1. piemērs

Ņemsim piemēru no mazumtirgotāja, kurš ir ieinteresēts uzzināt, cik daudz viņu klientu nopirka preci no viņiem pēc tam, kad noteiktā dienā bija apskatījuši viņu vietni. Ņemot vērā to, ka viņu vietnei ir vidēji 10 000 skatījumu dienā, nosakiet to klientu izlases lielumu, kuri viņiem jāuzrauga 95% ticamības līmenī ar 5% kļūdu robežu, ja:

• Viņi nav pārliecināti par pašreizējo konversijas likmi.
• Pēc iepriekšējām aptaujām viņi zina, ka reklāmguvumu līmenis ir 5%.

Ņemot vērā

• Iedzīvotāju skaits, N = 10 000
• Kritiskā vērtība pie 95% ticamības līmeņa, Z = 1,96
•  Kļūdu robeža, e = 5% vai 0,05

1 - Tā kā pašreizējais reklāmguvumu līmenis nav zināms, pieņemsim, ka p = 0,5

Tāpēc izlases lielumu var aprēķināt, izmantojot šādu formulu:

= (10 000 * (1,96 2) * 0,5 * (1-0,5) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,5 * (1-0,5) / (0,05 2))))

Tāpēc 370 klienti būs piemēroti, lai iegūtu jēgpilnu secinājumu.

2 - pašreizējais reklāmguvumu līmenis ir p = 5% vai 0,05

Tāpēc izlases lielumu var aprēķināt, izmantojot iepriekš minēto formulu kā:

= (10 000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Tāpēc 72 klientu lielums būs piemērots, lai šajā gadījumā iegūtu jēgpilnu secinājumu.

2. piemērs

Ņemsim iepriekš minēto piemēru un šajā gadījumā pieņemsim, ka populācijas lielums, ti, ikdienas vietnes skatījums, ir no 100 000 līdz 120 000, bet tad precīza vērtība nav zināma. Pārējās vērtības ir vienādas ar konversijas likmi 5%. Aprēķiniet izlases lielumu gan 100 000, gan 120 000.

Ņemot vērā

• Parauga proporcija, p = 0,05
• Kritiskā vērtība pie 95% ticamības līmeņa, Z = 1,96
•  Kļūdas robeža, e = 0,05

Tāpēc izlases lielumu N = 100 000 var aprēķināt kā

= (100000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (100000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Tāpēc izlases lielumu N = 120 000 var aprēķināt kā

= (120000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (120000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Tāpēc ir pierādīts, ka, palielinoties populācijas lielumam, ir ļoti liels, tas kļūst mazsvarīgs, aprēķinot izlases lielumu.

Atbilstība un lietojumi

Izlases lieluma aprēķins ir svarīgs, lai saprastu piemērota parauga lieluma jēdzienu, jo to izmanto pētījumu rezultātu pamatotībai. Ja tas ir pārāk mazs, tas nedos derīgus rezultātus, savukārt pārāk liels paraugs var izšķiest gan naudu, gan laiku. Statistiski ievērojamo izlases lielumu galvenokārt izmanto tirgus pētījumu apsekojumos, veselības aprūpes apsekojumos un izglītības apsekojumos.