seychellesartprojects.org

Efektīvas procentu likmes definīcija

Efektīvā procentu likme, kas pazīstama arī kā gada ekvivalenta likme, ir procentu likme, ko persona faktiski maksā vai nopelna par finanšu instrumentu un kuru aprēķina, ņemot vērā apvienošanās ietekmi laika periodā.

Efektīvā procentu likmju formula

Efektīvā procentu likmju formula = (1 + i / n) n -

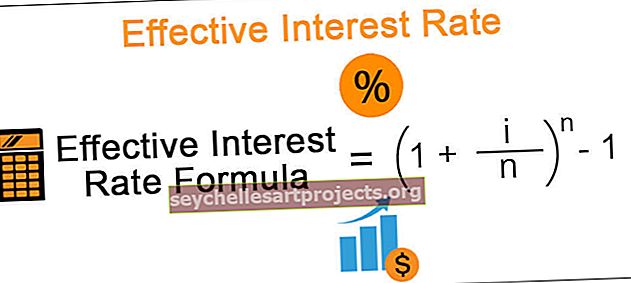
Šeit i = gada procentu likme, kas minēta instrumentā.

n = tas norāda salikšanas periodu skaitu gadā.

Interpretācijas

Salikšana maina procentu likmi. Tāpēc instrumentam noteiktā procentu likme ieguldītājam nav efektīva procentu likme (gada ekvivalenta likme). Piemēram, ja instrumentam tiek uzrakstīta 11% procentu likme un procentu likme tiek palielināta četras reizes gadā, tad gada ekvivalenta likme nevar būt 11%.

Kas tas būtu tad?

Tas būtu - (1 + i / n) n - 1 = (1 + 0,11 / 4) 4 - 1 = 1.1123 - 1 = 0.1123 = 11.23%.

Tas nozīmē, ka ieguldītāja faktiskā procentu likme būtu 11,23%.

Pat ja izmaiņas ir niecīgas, tās nav vienādas ar instrumentā minēto gada procentu likmi.

Piemērs

1. piemērs

Tings nopirka konkrētu instrumentu. Instrumentam pieminētā procentu likme ir 16%. Viņš ir ieguldījis aptuveni 100 000 USD. Instruments tiek savienots katru gadu. Kāda būtu šī konkrētā instrumenta faktiskā procentu likme (AER)? Cik viņš katru gadu iegūtu kā interesi?

Efektīvā procentu likme un gada likme ne vienmēr ir vienādas, jo procentus katru gadu palielina vairākas reizes. Dažreiz procentu likmi palielina pusgada, ceturkšņa vai mēneša laikā. Un tieši tā gada ekvivalenta likme atšķiras no gada procentu likmes.

Šis piemērs jums to parāda.

Aprēķināsim.

Tā kā procentu likme tiek palielināta katru gadu, šeit būtu efektīvās procentu likmes formula -

(1 + i / n) n - 1 = (1 + 0,16 / 1) 1 - 1 = 1,16 - 1 = 0,16 = 16%.

Tas nozīmē, ka šajā konkrētajā piemērā nebūtu atšķirības starp gada procentu likmi un gada ekvivalentu likmi (AER).

Katru gadu Tings iegūs procentus par = (100 000 USD * 16%) = 16 000 USD par instrumentu.

2. piemērs

Tongs nopirka konkrētu instrumentu. Instrumentam pieminētā procentu likme ir 16%. Viņš ir ieguldījis aptuveni 100 000 USD. Instruments tiek savienots sešas reizes gadā. Kāda būtu šī gada instrumenta ekvivalenta likme (AER)? Cik viņš katru gadu iegūtu kā interesi?

Tas ir tikai iepriekšējā piemēra pagarinājums.

Bet tur ir milzīga atšķirība.

Iepriekšējā piemērā instruments tika apvienots reizi gadā, kas gada procentu likmi padarīja līdzīgu gada ekvivalentajai likmei.

Tomēr šajā gadījumā scenārijs ir pilnīgi atšķirīgs.

Šeit mums ir procentu likme, kas tiek palielināta sešas reizes gadā.

Tātad, šeit ir gada procentu likmes formula -

(1 + i / n) n - 1 = (1 + 0,16 / 6) 6 - 1 = 1,171 - 1 = 0,171 = 17,1%.

Tagad jūs varat redzēt, ka, ja procentu likme tiek palielināta sešas reizes gadā, gada ekvivalentā likme kļūst pavisam citāda.

Tagad, kad mums ir efektīva procentu likme, mēs varam aprēķināt procentus, ko Tong iegūs gada beigās.

Tong iegūs = (100 000 USD * 17,1%) = 17 100 USD.

Ja salīdzinām procentus, kurus Ting iegūst iepriekšējā piemērā, ar Tong saņemšanu, jo procentu likmes atšķiras citādi, mēs redzēsim, ka procentu starpība ir aptuveni USD 1100.

3. piemērs

Ping ir ieguldījis instrumentu. Viņa ir ieguldījusi 10 000 USD. Instrumentā minētā procentu likme ir 18%. Procenti tiek apvienoti katru mēnesi. Uzziniet, kā pirmajā gadā Ping katru mēnesi saņems procentus.

Šis ir daudz detalizēts gada ekvivalenta likmes piemērs.

Šajā piemērā mēs parādīsim, kā faktiski notiek aprēķins, neizmantojot efektīvās procentu likmes formulu.

Paskatīsimies.

Tā kā procentu likme tiek apvienota katru mēnesi, minētās procentu likmes faktiskais sadalījums mēnesī ir = (18/12) = 1,5%.

• Pirmajā mēnesī Ping saņems procentus = (10 000 * 1,5%) = 150 USD.
• Otrajā mēnesī Pings saņems procentus = {(10 000 + 150) * 1,5%} = (10 150 * 1,5%) = 152,25 USD.
• Trešajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25) * 1,5%} = (10 302,25 * 1,5%) = 154,53 USD.
• Ceturtajā mēnesī Ping saņems procentus = {(10 000 + 150 + 152,25 + 154,53) * 1,5%} = (10 456,78 * 1,5%) = 156,85 USD.
• Piektajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85) * 1,5%} = (10 613,63 * 1,5%) = 159,20 USD.
• Sestajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20) * 1,5%} = (10 772,83 * 1,5%) = 161,59 USD.
• Septītajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59) * 1,5%} = (10 934,42 * 1,5%) = 164,02 USD.
• Astotajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02) * 1,5%} = (11098,44 * 1,5%) = 166,48 USD.
• Devītajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48) * 1,5%} = (11264,92 * 1,5%) = 168,97 USD.
• Desmitajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97) * 1,5%} = (11433,89 * 1,5%) = 171,51 USD.
• Vienpadsmitajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51) * 1,5%} = (11605,40 * 1,5%) = 174,09 USD.
• Divpadsmitajā mēnesī Pings saņems procentus = {(10 000 + 150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09) * 1,5%} = (11779,49 * 1,5%) = 176,69 ASV dolāri.

Kopējā interese, ko Pings ieguva par gadu, ir -

• (150 + 152,25 + 154,53 + 156,85 + 159,20 + 161,59 + 164,02 + 166,48 + 168,97 + 171,51 + 174,09 + 176,69) = 1956,18 ASV dolāri.

• Gada ekvivalenta likmes formula = (1 + i / n) n - 1 = (1 + 0,18 / 12) 12 - 1 = 1,195618 - 1 = 0,1951818 = 19,5618%.

Tātad procentus, ko Pings saņems = (10 000 USD ^ 19,5618%) = 1956,18 USD.

Efektīva procentu likme programmā Excel

Lai atrastu efektīvo procentu likmi vai gada ekvivalentu likmi programmā Excel, mēs izmantojam excel funkciju EFFECT.

• nominal_rate ir procentu likme
• nper ir salikšanas periodu skaits gadā

Apskatīsim zemāk redzamo piemēru

• Ja jūsu nominālā procentu likme ir 10% gadā, tad gada ekvivalenta likme ir tāda pati kā 10%.
• Ja jūsu nominālā procentu likme ir 10%, kas tiek palielināta sešus mēnešus, tad gada ekvivalenta likme ir tāda pati kā 10,25%.
• Ja jūsu nominālā procentu likme ir 10%, kas tiek apvienota reizi ceturksnī, tad gada ekvivalenta likme ir tāda pati kā 10,38%.
• Ja jūsu nominālā procentu likme ir 10% mēnesī, tad gada ekvivalenta likme ir tāda pati kā 10,47%.
• Ja jūsu nominālā procentu likme ir 10% katru dienu, faktiskā procentu likme ir tāda pati kā 10,52%.

Ieteiktie lasījumi

Tas bija efektīvās procentu likmes un tās definīcijas ceļvedis. Šeit mēs apspriežam efektīvās procentu likmes formulu kopā ar pakāpeniskiem aprēķiniem. Lai uzzinātu vairāk, varat atsaukties uz šādiem rakstiem

• Negatīvās procentu likmes piemērs
• Aprēķiniet dalības līmeni
• Atšķirības - diskonta likme pret procentu likmi
• Nominālā procentu likmju formula
• Cointegration
<