seychellesartprojects.org

Kas ir vidējais harmoniskais?

Harmoniskais vidējais ir abpusējais aritmētiskā vidējā aritmētiskajam, ti, vidējo aprēķina, dalot novērojumu skaitu dotajā datu kopā ar tā savstarpējo summu (1 / Xi) katram novērojumam dotajā datu kopā.

Vidējā harmoniskā formula

Harmoniskais vidējais = n / ∑ [1 / X _i ]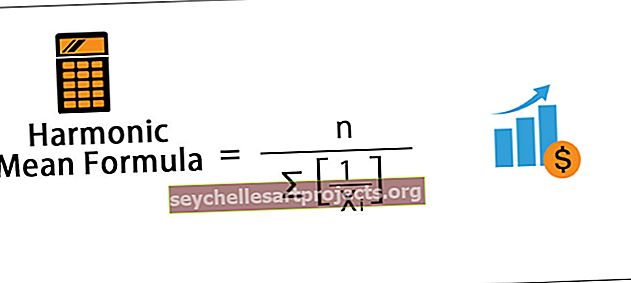

• Var redzēt, ka tas ir normālā vidējā rādītāja atgriezeniskā vērtība.
• Parastā vidējā harmoniskā vidējā vērtība ir ∑ x / n, tāpēc, ja formula tiek mainīta pretēji, tā kļūst par n / andx, un tad visām izmantotā saucēja vērtībām jābūt abpusējām, ti, skaitītājam tas paliek “n”, bet skaitlim saucējs vērtības vai to novērojumi, kas mums jāizmanto savstarpējām vērtībām.
• Atvasinātā vērtība vienmēr būtu mazāka par vidējo vai teiktu vidējo aritmētisko.

Piemēri

Šo Harmonic Mean Formula Excel veidni varat lejupielādēt šeit - Harmonic Mean Formula Excel veidne

1. piemērs

Apsveriet šādu skaitļu datu kopu: 10, 2, 4, 7. Izmantojot iepriekš apspriesto formulu, jums jāaprēķina vidējais harmoniskais.

Risinājums:

Aprēķinam izmantojiet šādus datus.

Vidējais harmoniskais = n / ∑ [1 / X _i ]

= 4 / (1/10 + 1/2 + 1/4 + 1/7)

= 4 / 0,99

2. piemērs

Vijay kungs ir JP Morgan akciju analītiķis. Viņa menedžeris ir lūdzis viņu noteikt indeksa P / E attiecību, kas izseko uzņēmuma W, uzņēmuma X un uzņēmuma Y akciju cenas. Uzņēmums W ziņo par peļņu 40 miljonu ASV dolāru apmērā un tirgus kapitalizāciju par 2 miljardiem ASV dolāru. USD 3 miljardi un tirgus kapitalizācija 9 miljardu ASV dolāru apmērā, un, kamēr Y uzņēmums ziņo par peļņu 10 miljardu ASV dolāru apmērā un tirgus kapitalizāciju 40 miljardu ASV dolāru apmērā. Aprēķiniet indeksa P / E attiecības vidējo harmonisko.

Risinājums:

Aprēķinam izmantojiet šādus datus

Pirmkārt, mēs aprēķināsim P / E attiecību

P / E koeficients būtībā ir (tirgus kapitalizācija / peļņa).

• (Uzņēmuma W) P / E = (2 miljardi USD) / (40 miljoni USD) = 50
• (Uzņēmuma X) P / E = (9 miljardi USD) / (3 miljardi USD) = 3
• (Uzņēmuma Y) P / E = (40 miljardi USD) / (10 miljardi USD) = 4

1 / X vērtības aprēķināšana

• Uzņēmums W = 1/50 = 0,02
• Uzņēmums X = 1/3 = 0,33
• Uzņēmums Y = 1/4 = 0,25

Aprēķinu var veikt šādi:

Vidējais harmoniskais = n / ∑ [1 / X _i ]

• = 3 / (1/50 + 1/3 + 1/4)
• = 3 / 0,60

3. piemērs

Rejs, Kalifornijas ziemeļu iedzīvotājs, ir profesionāls sporta riteņbraucējs un svētdienas vakarā ap pulksten 17:00 pēc EST dodas ekskursijā uz pludmali no savām mājām. Viņš brauc ar savu velosipēdu ar ātrumu 50 jūdzes stundā brauciena pirmajā pusē un 70 jūdzes stundā otrajā pusē no mājām līdz pludmalei. Kāds būs viņa vidējais ātrums?

Risinājums:

Aprēķinam izmantojiet šādus datus.

Šajā piemērā Rejs devās ceļojumā ar noteiktu ātrumu, un šeit vidējais rādītājs būtu atkarīgs no attāluma.

Aprēķinu var veikt šādi:

Šeit mēs varam aprēķināt vidējo harmonisko vidējo ātrumu Rei sporta velosipēdam.

Vidējais harmoniskais = n / ∑ [1 / X _i ]

• = 2 / (1/50 + 1/70)
• = 2 / 0,03

Reija sporta velosipēda vidējais ātrums ir 58,33.

Izmantošana un atbilstība

Harmoniskie līdzekļi, tāpat kā citas vidējās formulas, arī viņiem ir vairāki lietojumi, un tos galvenokārt izmanto finanšu jomā, lai vidēji noteiktu datus, piemēram, cenu reizinājumus. Finanšu reizinātājus, piemēram, P / E koeficientu, nedrīkst aprēķināt, izmantojot parasto vidējo vai vidējo aritmētisko, jo šie vidējie rādītāji ir tendenciozi pret lielākām vērtībām. Harmoniskos līdzekļus var arī izmantot, lai identificētu noteikta veida modeļus, piemēram, Fibonači secības, kuras galvenokārt izmanto tehnisko analīzi veic tirgus tehniķi.

Harmoniskais vidējais rādītājs attiecas arī uz tādu vienību vidējiem rādītājiem kā likmes, proporcijas vai ātrums utt. Ir arī svarīgi atzīmēt, ka to ietekmē galējās vērtības dotajā datu kopā vai noteiktā novērojumu komplektā.

Harmoniskais vidējais ir noteikts stingri, un tā pamatā ir visas vērtības vai visi novērojumi dotajā datu kopā vai paraugā, un tas var būt piemērots turpmākai matemātiskai apstrādei. Tāpat kā ģeometriskais vidējais, arī harmonisko vidējo daudz neietekmē novērojumu vai paraugu ņemšanas svārstības. Tas piešķirtu lielāku nozīmi mazajām vērtībām vai mazajiem novērojumiem, un tas būs noderīgi tikai tad, kad šīm mazajām vērtībām vai mazajiem novērojumiem būs jāpiešķir lielāks svars.