seychellesartprojects.org

Kas ir R kvadrāts (R2) regresijā?

R kvadrāts (R2) ir svarīgs statistikas rādītājs, kas ir regresijas modelis, kas statistiskā izteiksmē parāda starpības vai dispersijas proporciju atkarīgajam mainīgajam, ko var izskaidrot ar neatkarīgu mainīgo vai mainīgajiem. Īsāk sakot, tas nosaka, cik labi dati derēs regresijas modelim.

R Formula kvadrātā

Lai aprēķinātu R kvadrātu, jānosaka korelācijas koeficients, un pēc tam rezultāts ir kvadrātā.

R kvadrāta formula = r2

Kur r korelācijas koeficientu var aprēķināt zemāk:

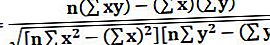
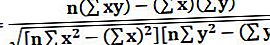
Kur,

• r = korelācijas koeficients
• n = skaitlis dotajā datu kopā
• x = pirmais mainīgais kontekstā
• y = otrais mainīgais

Paskaidrojums

Ja starp šiem diviem mainīgajiem lielumiem ir kāda sakarība vai korelācija, kas var būt lineāra vai nelineāra, tad tas norāda, vai mainās vērtības neatkarīgais mainīgais, tad otrs atkarīgais mainīgais, visticamāk, mainīsies vērtībā, teiksim lineāri vai nelineāri. lineāri.

Formulas skaitītāja daļa veic pārbaudi, vai viņi pārvietojas kopā, un noņem viņu individuālās kustības un abu kustīgo relatīvo spēku, un formulas saucēja daļa mērogo skaitītāju, ņemot kvadrātsakni no produkta atšķirību reizinājuma. mainīgie no to mainīgajiem kvadrātā. Kad jūs kvadrātiet šo rezultātu, mēs iegūstam R kvadrātu, kas ir nekas cits kā noteikšanas koeficients.

Piemēri

Šo R kvadrāta formulas Excel veidni varat lejupielādēt šeit - R kvadrāta formulas Excel veidne

1. piemērs

Apsveriet šādus divus mainīgos x un y, jums jāaprēķina R kvadrāts regresijā.

Risinājums:

Izmantojot iepriekš minēto formulu, mums vispirms jāaprēķina korelācijas koeficients.

Mums ir visas iepriekšminētās tabulas vērtības ar n = 4.

Tagad ievadīsim formulas vērtības, lai iegūtu skaitli.

r = (4 * 26 046,25) - (265,18 * 326,89) / √ [(4 * 21 274,94) - (326,89) 2] * [(4 * 31 901,89) - (326,89) 2]

r = 17 501,06 / 17 512,88

Korelācijas koeficients būs

r = 0,99932480

Tātad aprēķins būs šāds,

r2 = (0,99932480) 2

R kvadrāta formula regresijā

r2 = 0,998650052

2. piemērs

Indija, jaunattīstības valsts, vēlas veikt neatkarīgu analīzi, vai jēlnaftas cenu izmaiņas ir ietekmējušas tās rūpijas vērtību. Tālāk ir parādīta Brent jēlnaftas cenas un rūpijas vērtēšanas vēsture gan attiecībā pret dolāriem, kas vidēji šajos gados dominēja zemāk.

Indijas centrālā banka RBI ir vērsusies pie jums, lai nākamajā sanāksmē sniegtu prezentāciju par to pašu. Nosakiet, vai jēlnaftas kustība ietekmē rūpijas kustību par dolāru?

Risinājums:

Izmantojot iepriekšminētās korelācijas formulu, vispirms varam aprēķināt korelācijas koeficientu. Apstrādājot jēlnaftas vidējo cenu kā vienu mainīgo, saka x, un rūpiju par dolāru uzskatot par citu mainīgo kā y.

Mums ir visas iepriekšminētās tabulas vērtības ar n = 6.

Tagad ievadīsim formulas vērtības, lai iegūtu skaitli.

r = (6 * 23592,83) - (356,70 * 398,59) / √ [(6 * 22829,36) - (356,70) 2] * [(6 * 26529,38) - (398,59) 2]

r = -620,06 / 1,715,95

Korelācijas koeficients būs

r = -0,3614

Tātad aprēķins būs šāds,

r2 = (-0,3614) 2

R kvadrāta formula regresijā

r2 = 0,1306

Analīze. Šķiet, ka starp jēlnaftas cenu izmaiņām un Indijas rūpijas cenas izmaiņām ir neliela saistība. Pieaugot jēlnaftas cenai, ietekmē arī Indijas rūpijas izmaiņas. Bet, tā kā R kvadrāts ir tikai 13%, tad jēlnaftas cenas izmaiņas izskaidro mazāk par Indijas rūpijas izmaiņām, un Indijas rūpija ir pakļauta izmaiņām arī citos mainīgos lielumos, par kuriem jāņem vērā.

3. piemērs

XYZ laboratorija veic auguma un svara izpēti un ir ieinteresēta uzzināt, vai starp šiem mainīgajiem ir kāda veida saistība. Pēc katras kategorijas 5000 cilvēku izlases apkopošanas un nāca klajā ar vidējo svaru un vidējo augstumu šajā konkrētajā grupā.

Tālāk ir sniegta informācija, ko viņi ir apkopojuši.

Jums jāaprēķina R kvadrāts un jāsecina, ja šis modelis izskaidro augstuma dispersijas ietekmē svara variācijas.

Risinājums:

Izmantojot iepriekšminētās korelācijas formulu, vispirms varam aprēķināt korelācijas koeficientu. Apstrādājot augstumu kā vienu mainīgo, sakiet x un svaru kā citu mainīgo kā y.

Mums ir visas iepriekšminētās tabulas vērtības ar n = 6.

Tagad ievadīsim formulas vērtības, lai iegūtu skaitli.

r = (7 * 74 058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6581,05 / 7075,77

Korelācijas koeficients būs

Korelācijas koeficients (r) = 0,930

Tātad aprēķins būs šāds,

r2 = 0,865

Analīze: korelācija ir pozitīva, un šķiet, ka pastāv zināma saistība starp augumu un svaru, jo augums palielina arī cilvēka svaru. Lai gan R2 norāda, ka 86% auguma izmaiņu ir saistītas ar svara izmaiņām un 14% ir neizskaidrojamas.

Atbilstība un lietojumi

R kvadrāta atbilstība regresijā ir tā spēja atrast nākotnes notikumu iespējamību dotajos prognozētajos rezultātos vai iznākumos. Ja modelim pievieno vairāk paraugu, koeficients parādīs varbūtību vai varbūtību, ka jauns punkts vai jaunā datu kopa nokritīs uz līnijas. Pat ja abiem mainīgajiem ir cieša saikne, noteikšana nepierāda cēloņsakarību.

Dažas vietas, kur lielākoties tiek izmantots R kvadrāts, ir kopfondu darbības izsekošanai, riska ieguldījumu fondu riska izsekošanai, lai noteiktu, cik labi akcijas pārvietojas ar tirgu, kur R2 ieteiktu, cik lielu daļu no akciju kustībām var izskaidrot. ko nosaka tirgus kustības.