seychellesartprojects.org

Vismazāko kvadrātu regresijas metodes definīcija

Mazāko kvadrātu regresijas metode ir regresijas analīzes forma, kas nosaka saistību starp atkarīgo un neatkarīgo mainīgo kopā ar lineāru līniju. Šī līnija tiek dēvēta par “vispiemērotākās līniju”.

Regresijas analīze ir statistikas metode, ar kuras palīdzību var noteikt vai paredzēt viena mainīgā nezināmās vērtības no cita mainīgā zināmām vērtībām. Mainīgo, kas tiek izmantots, lai prognozētu mainīgo procentu, sauc par neatkarīgo vai paskaidrojošo mainīgo, bet mainīgo, par kuru tiek prognozēts, sauc par atkarīgo vai izskaidroto mainīgo.

Apsvērsim divus mainīgos x & y. Tie ir uzzīmēti grafikā ar x vērtībām uz x ass vērtībām y uz y ass. Šīs vērtības ir attēlotas ar punktiem zemāk redzamajā diagrammā. Caur punktiem tiek novilkta taisna līnija, kas tiek dēvēta par vispiemērotāko līniju.

Mazāko kvadrātu regresijas mērķis ir nodrošināt, lai caur sniegto vērtību kopu novilktā līnija izveidotu visciešāko saistību starp vērtībām.

Vismazāko kvadrātu regresijas formula

Regresijas līniju zemāko kvadrātu metodē aprēķina, izmantojot šādu formulu:

ŷ = a + bx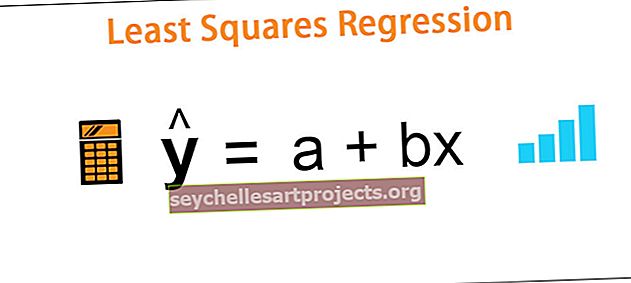

Kur,

• dependent = atkarīgs mainīgais
• x = neatkarīgs mainīgais
• a = y pārtveršana
• b = līnijas slīpums

B līnijas slīpumu aprēķina, izmantojot šādu formulu:

Or

Y-pārtverto vērtību “a” aprēķina, izmantojot šādu formulu:

Vislabākā fit līnija vismazākā laukuma regresijā

Vislabāk piemērotā līnija ir taisna līnija, kas novilkta caur datu punktu izkliedi un vislabāk atspoguļo attiecības starp tām.

Apsvērsim šo grafiku, kurā datu kopa ir uzzīmēta gar x un y asi. Šie datu punkti tiek attēloti, izmantojot zilos punktus. Caur šiem punktiem ir novilktas trīs līnijas - zaļa, sarkana un zila. Zaļā līnija iet caur vienu punktu un sarkanā līnija iet caur trim datu punktiem. Tomēr zilā līnija iet caur četriem datu punktiem, un attālums starp atlikušajiem punktiem līdz zilajai līnijai ir minimāls, salīdzinot ar pārējām divām līnijām.

Iepriekš redzamajā diagrammā zilā līnija apzīmē vispiemērotāko līniju, jo tā atrodas vistuvāk visām vērtībām, un attālums starp punktiem ārpus līnijas līdz līnijai ir minimāls (ti, attālums starp atlikumiem līdz vislabākās atbilstības līnijai - dēvē arī par atlikumu kvadrātu summām). Divās pārējās līnijās - oranžā un zaļā - attālums starp atlikumiem līdz līnijām ir lielāks, salīdzinot ar zilo līniju.

Mazāko kvadrātu metode nodrošina visciešāko saistību starp atkarīgajiem un neatkarīgajiem mainīgajiem, samazinot attālumu starp atlikumiem un vislabāk piemēroto līniju, ti, šajā pieejā atlieku kvadrātu summa ir minimāla. No tā izriet termins “vismazākie kvadrāti”.

Vismazāko kvadrātu regresijas līnijas piemēri

Izmantosim šīs formulas zemāk esošajā jautājumā -

Šo Vismazāko kvadrātu regresijas Excel veidni varat lejupielādēt šeit - Vismazāko kvadrātu regresijas Excel veidne

1. piemērs

Sīkāka informācija par tehniķu pieredzi uzņēmumā (vairāku gadu laikā) un viņu darbības vērtējumu ir sniegta zemāk esošajā tabulā. Izmantojot šīs vērtības, novērtējiet tehniķa ar 20 gadu pieredzi veiktspēju.

Risinājums -

Lai aprēķinātu vismazāk kvadrātu, vispirms aprēķināsim Y līnijas krustojumu (a) un līnijas (b) slīpumu šādi:

B līnijas slīpums

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1,13

Y pārtveršana (a)

• a = 648 - (1,13) (80) / 8
• = 69,7

Regresijas līniju aprēķina šādi:

Formulā x vērtību aizstājot ar 20,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• ŷ = 92,3

Tiek lēsts, ka tehniķa ar 20 gadu pieredzi sniegums ir 92,3.

2. piemērs

Vismazāko kvadrātu regresijas vienādojums, izmantojot programmu Excel

Mazāko kvadrātu regresijas vienādojumu var aprēķināt, izmantojot Excel, veicot šādas darbības:

• Ievietojiet datu tabulu programmā Excel.

• Izmantojot datu punktus, ievietojiet izkliedes diagrammu.

• Ievietojiet tendenču līniju izkliedes diagrammā.

• Zem tendenču līnijas opcijām atlasiet lineāru tendenču līniju un atlasiet diagrammas attēlojuma vienādojumu.

• Vismazāko kvadrātu regresijas vienādojums dotajai Excel datu kopai tiek parādīts diagrammā.

Tādējādi tiek aprēķināts mazākā kvadrāta regresijas vienādojums dotajam Excel datu kopumam. Izmantojot vienādojumu, var veikt prognozes un tendenču analīzi. Excel rīki nodrošina arī detalizētus regresijas aprēķinus.

Priekšrocības

• Regresijas analīzes mazāko kvadrātu metode ir vislabāk piemērota prognozēšanas modeļiem un tendenču analīzei. Vislabāk to izmantot ekonomikas, finanšu un akciju tirgos, kur jebkura nākotnes mainīgā vērtība tiek prognozēta, izmantojot esošos mainīgos un savstarpējo saistību.
• Mazāko kvadrātu metode nodrošina visciešāko saistību starp mainīgajiem. Atšķirība starp atlikumu kvadrātu summām ar vislabākās atbilstības līniju šajā metodē ir minimāla.
• Aprēķina mehānisms ir vienkāršs un viegli pielietojams.

Trūkumi

• Mazāko kvadrātu metode balstās uz tuvākās attiecības noteikto mainīgo kopu izveidi. Aprēķina mehānisms ir jutīgs pret datiem, un, ja tiek ņemti vērā ārkārtas gadījumi (izņēmuma dati), rezultāti var būt tendence būtiski ietekmēt.
• Šāda veida aprēķini ir vislabāk piemēroti lineāriem modeļiem. Nelineāriem vienādojumiem tiek izmantoti izsmeļošāki skaitļošanas mehānismi.

Secinājums

Mazāko kvadrātu metode ir viena no populārākajām metodēm prognozēšanas modeļiem un tendenču analīzei. Ja tas tiek pareizi aprēķināts, tas nodrošina vislabākos rezultātus.