seychellesartprojects.org

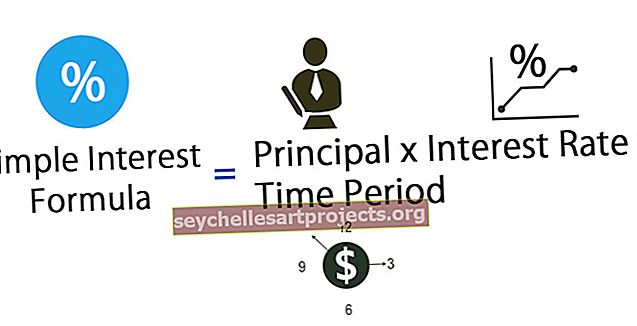
Formula vienkāršās procentu aprēķināšanai (SI)

Vienkāršie procenti (SI) ir veids, kā aprēķināt procentu summu, kas jāmaksā par pamatsummu, un tiek aprēķināta pēc vienkāršas formulas, kas ir, reizinot pamatsummu ar procentu likmi un periodu skaitu, par kuriem jāmaksā procenti.

Šeit procentus aprēķina tikai par sākotnēji ieguldīto summu, un procentiem nav procentu, kā tas ir gadījumā ar salikto procentu formulu. Tas tiek izmantots aizdevumos ar automašīnu un citos patēriņa aizdevumos, ko izsniedz bankas un finanšu iestādes. Arī procenti, ko maksā par krājbanku kontiem un termiņnoguldījumiem, balstās uz vienkāršiem procentiem.

Piemēri

Šo vienkāršās procentu formulas Excel veidni varat lejupielādēt šeit - vienkāršās procentu formulas Excel veidne

1. piemērs

ABC aizdod 5000 USD summu ar 10% gadā uz 5 gadu periodu. Aprēķiniet vienkāršos procentus un kopējo summu, kas jāmaksā pēc 5 gadiem.

Galvenais: 5000 USD

Procentu likme: 10% gadā

Laika periods (gados) = 5

Tātad tagad mēs to aprēķināsim, izmantojot vienkāršo procentu vienādojumu, ti

• Vienkāršā procentu likme = galvenā * procentu likme * laika periods
• Vienkāršā procentu likme = $ 5000 * 10% * 5
• = 2500 USD

Kopējā vienkāršā procentu likme 5 gadus = 2500 USD

Pēc 5 gadiem maksājamā summa = pamatsumma + vienkāršie procenti

• = 5000 USD + 2500 USD
• Pēc 5 gadiem maksājamā summa = 7500 USD.

2. piemērs

Ravi iegādājās mikroviļņu krāsni elektronikas veikalā, kura cena ir 10000 Rs. To pašu viņš finansēja no aizdevēja HDFC bankas. Sīkāka informācija:

aizdevuma summa: Rs 12000

aizdevuma periods: 1 gads

procenti: 10% gadā

Maksājumu biežums: katru mēnesi

Izmantojot PMT funkciju, mēs varam aprēķināt pielīdzināto mēneša summu Excel.

Attiecīgi EMI summa, kas Ravi būs jāmaksā, sasniedz 879,16 rs (kas ietver gan procentus, gan pamatsummu). No zemāk redzamā hipotēkas amortizācijas grafika mēs varam vienkārši novērot, ka procentu summa ar katru maksājumu samazinājās un pamatsumma turpināja pieaugt; tomēr ikmēneša maksājums visā aizdevuma darbības laikā palika nemainīgs.

Svarīgi punkti, kas jāņem vērā, aprēķinot vienkāršos procentus:

• Laika periodam jābūt gados. Gadījumā, ja tas pats notiek mēnesī, tas jāpārvērš gados kā daļa.
• Procentu likme jāizsaka gadā, bet, ja laika periods ir mazāks par gadu, tā jāpielāgo par vienu gadu. Piemēram, ja procentu likme ir 12% gadā, bet problēma ir saistīta ar mēneša procentu likmi, tā būs 1% (12% / 12).

3. piemērs

Rams no HDBC bankas paņēma automašīnas aizdevumu 500 000 ASV dolāru apmērā, kur procenti maksājami par 10% par 24 mēnešu periodu. Aizdevums ir jāatmaksā, veicot ikmēneša vienādus maksājumus USD 23072,46 (aprēķināts, izmantojot Excel PMT funkciju)

Maksājumu grafiks, kas aprēķināts, izmantojot Excel formulu programmā Excel, ir šāds:

Izpratīsim SI formulas jēdzienu excel, izmantojot vēl vienu nozares piemēru, kas saistīts ar noguldījumu sertifikātu (CD).

4. piemērs

ABC Bank parakstījās uz Indijas valdības izsniegto noguldījumu sertifikātu 20000 USD vērtībā, kuram ir 5% procenti gadā. Noguldījumu sertifikāta termiņš ir 6 mēneši.

ABC Bank nopelnītie procenti par noguldījumu sertifikātu:

Vienkāršā procentu likme = galvenā * likme * laika periods

Tādējādi ABC Bank nopelnīs noguldījumu sertifikātu kopējos procentus USD 500 apmērā pēc termiņa beigām, ti, pēc 6 mēnešiem.

Vienkāršs procentu kalkulators

Varat izmantot šo vienkāršo procentu kalkulatoru.

Direktors
Procentu likme
Laika periods
Vienkāršā procentu formula =

Vienkāršā procentu formula =	Pamatsumma x Procentu likme x Laika periods
	0 x 0 x 0 =	0

Atbilstība un lietojumi

• Vienkāršajiem procentiem ir nozīme, kā bankas aprēķina procentus par krājbankas kontu un noguldītāju turētajiem termiņnoguldījumiem. Parasti bankas uzkrājumos un termiņnoguldījumos aprēķina procentus reizi ceturksnī.
• Atdeve, kas aprēķināta saskaņā ar vienkāršajiem procentiem, vienmēr būs mazāka nekā peļņa, kas aprēķināta saskaņā ar saliktajiem procentiem, jo ​​tā ignorē salikšanas jēdzienu.
• SI formula nodrošina, ka procentu daļa sākotnējos gados ir augstāka un pēc tam samazināta, ņemot vērā aizdevuma termiņu.
• To izmanto, lai aprēķinātu procentus par īstermiņa aizdevumiem, piemēram, automašīnu aizdevumiem, noguldījumu sertifikātiem, krājkontiem un termiņnoguldījumiem.