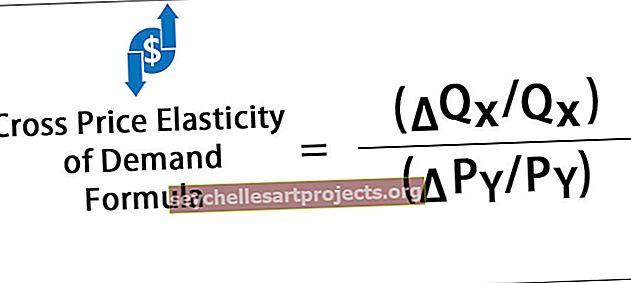
P vērtības formula | Soli pa solim piemēri P vērtības aprēķināšanai
Kas ir P-vērtības formula?
P ir statistikas mērs, kas palīdz pētniekiem noteikt, vai viņu hipotēze ir pareiza. Tas palīdz noteikt rezultātu nozīmīgumu. Nulles hipotēze ir noklusējuma pozīcija, ka starp divām izmērītām parādībām nav sakarības. To apzīmē ar H 0. Alternatīva hipotēze ir tā, kurai jūs ticētu, ja nulles hipotēze tiek atzīta par nepatiesu. Tās simbols ir H 1 vai H a.
P vērtība excel ir skaitlis no 0 līdz 1. Lai aprēķinātu p vērtību, ir tabulas, izklājlapu programmas un statistikas programmatūra. Nozīmības līmenis (α) ir iepriekš noteikts slieksnis, ko nosaka pētnieks. Parasti tas ir 0,05. Ļoti maza p vērtība, kas ir mazāka par nozīmīguma līmeni, norāda, ka jūs noraidāt nulles hipotēzi. P vērtība, kas ir lielāka par nozīmības līmeni, norāda, ka mēs nespējam noraidīt nulles hipotēzi.
P-vērtības formulas skaidrojums
P vērtības aprēķināšanas formulu var iegūt, izmantojot šādas darbības:
P vērtības aprēķināšana no Z statistikas
1. solis: mums jānoskaidro testa statistika z

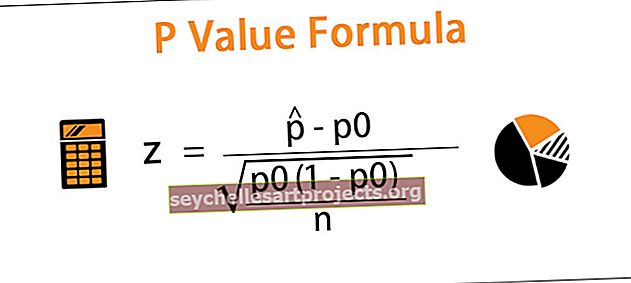
Kur
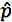 ir parauga proporcija
ir parauga proporcija- p0 ir pieņemtā populācijas proporcija nulles hipotēzē
- n ir izlases lielums
2. solis: Mums no iegūtās z vērtības jāatrod atbilstošais p līmenis. Šim nolūkam mums jāaplūko z tabula.

Avots: www.dummies.com
Piemēram, atradīsim p vērtību, kas atbilst z ≥ 2,81. Tā kā normālais sadalījums ir simetrisks, negatīvās z vērtības ir vienādas ar tā pozitīvajām vērtībām. 2,81 ir 2,80 un 0,01 summa. Skatiet z kolonnā 2.8 un atbilstošo vērtību 0.01. Mēs iegūstam p = 0,0025.
P-vērtības formulas piemēri (ar Excel veidni)
Apskatīsim dažus vienkāršus un uzlabotus P-vērtības vienādojuma piemērus, lai to labāk izprastu.
Šo P Value Formula Excel veidni varat lejupielādēt šeit - P Value Formula Excel veidne
1. piemērs
a) P vērtība ir 0,3015. Ja nozīmīguma līmenis ir 5%, atrodiet, vai mēs varam noraidīt nulles hipotēzi.
b) P vērtība ir 0,0129. Ja nozīmīguma līmenis ir 5%, atrodiet, vai mēs varam noraidīt nulles hipotēzi.
Risinājums:
P vērtības aprēķināšanai izmantojiet šādus datus.

P vērtība būs -

a) Tā kā p vērtība 0,3015 ir lielāka par nozīmības līmeni 0,05 (5%), mēs nevaram noraidīt nulles hipotēzi.
b) Tā kā p vērtība 0,01129 ir mazāka par nozīmības līmeni 0,05, mēs noraidām nulles hipotēzi.
2. piemērs
Pētījumā 27% cilvēku Indijā runā hindi valodā. Pētniekam ir interesanti, vai viņa ciematā šis skaitlis ir lielāks. Tādējādi viņš izveido nulles un alternatīvās hipotēzes. Viņš pārbauda H 0: p = 0,27. H a: p> 0,27. Šeit p ir to cilvēku īpatsvars ciematā, kuri runā hindi valodā. Viņš savā ciematā uzdod veikt aptauju, lai noskaidrotu cilvēku skaitu, kuri prot runāt hindi valodā. Viņš atklāj, ka 80 no 240 izlasē iekļautajiem cilvēkiem var runāt hindi valodā. Uzziniet aptuveno p vērtību pētnieka testam, ja mēs pieņemam, ka nepieciešamie nosacījumi ir izpildīti un nozīmīguma līmenis ir 5%.
Risinājums:
P vērtības aprēķināšanai izmantojiet šādus datus.

Šeit izlases lielums n = 240,
p 0 ir iedzīvotāju proporcija Mums būs jāatrod izlases proporcija
= 80/240
 = 0,33
= 0,33
Z Statistika
Z statistikas aprēķins


= 0,33 - 0,27 / √ 0,27 * (1 - 0,27) / 240
Z statistika būs -

Z = 2,093696
P vērtība būs -

P vērtība = P (z ≥ 2,09)
Mums ir jāaplūko vērtība 2.09 ir z tabula. Tātad, mums jāaplūko -2,0 z kolonnā un vērtība 0,09 kolonnā. Tā kā normālais sadalījums ir simetrisks, laukums pa labi no līknes ir vienāds ar kreiso. Mēs iegūstam p vērtību kā 0,0183.
P vērtība = 0,0183
Tā kā p vērtība ir mazāka par nozīmīgo 0,05 (5%) līmeni, mēs noraidām nulles hipotēzi.
Piezīme: Programmā Excel p-vērtība nāk kā 0,0181
3. piemērs
Pētījumi rāda, ka vīrieši iegādājas lielāku skaitu lidojuma biļešu nekā sievietes. Tos pērk vīrieši un sievietes proporcijā 2: 1. Pētījums tika veikts noteiktā Indijas lidostā, lai noskaidrotu aviobiļešu sadalījumu starp vīriešiem un sievietēm. No 150 biļetēm 88 biļetes iegādājās vīrieši, bet 62 - sievietes. Mums jānoskaidro, vai eksperimentālā manipulācija izraisa izmaiņas rezultātos, vai arī mēs novērojam iespēju variācijas. Aprēķiniet p vērtību, pieņemot, ka nozīmīguma pakāpe ir 0,05.
Risinājums:
P vērtības aprēķināšanai izmantojiet šādus datus.

1. solis: novērotā vērtība ir 88 vīriešiem un 62 sievietēm.
- Paredzamā vērtība vīriešiem = 2/3 * 150 = 100 vīrieši
- Paredzamā vērtība sievietēm = 1/3 * 150 = 50 sievietes
2. solis: uzziniet chi-square


= ((88-100) 2) / 100 + (62-50) 2/50
= 1,44 + 2,88
Či laukums (X ^ 2)
Či laukums (X ^ 2) būs -

Ši-kvadrāts (X ^ 2) = 4,32
3. solis: atrodiet brīvības pakāpes
Tā kā ir 2 mainīgie - vīrieši un sievietes, n = 2
Brīvības pakāpes = n-1 = 2-1 =
4. solis: No p-vērtību tabulas mēs skatāmies uz tabulas pirmo rindu, jo brīvības pakāpe ir 1. Mēs varam redzēt, ka p-vērtība ir no 0,025 līdz 0,05. Tā kā p vērtība ir mazāka par nozīmīguma pakāpi 0,05, mēs noraidām nulles hipotēzi.
P vērtība būs -

P vērtība = 0,037666922
Piezīme: Excel tieši piešķir p-vērtību, izmantojot formulu:
CHITEST (faktiskais diapazons, paredzamais diapazons)
4. piemērs
Ir zināms, ka 60% cilvēku, kas ienāk apģērbu veikalos pilsētā, kaut ko iegādājas. Apģērbu veikala īpašnieks vēlējās noskaidrot, vai viņam piederošo apģērbu veikala skaits ir lielāks. Viņam jau bija veikti veikala pētījuma rezultāti. 128 no 200 cilvēkiem, kuri ienāca viņa veikalā, kaut ko iegādājās. Veikala īpašnieks apzīmēja pas cilvēku skaitu, kuri ienāca viņa apģērbu veikalā un kaut ko iegādājās. Viņa formulētā nulles hipotēze bija p = 0,60 un alternatīvā hipotēze bija p> 0,60. Atrodiet p vērtību pētījumam ar nozīmības līmeni 5%.
Risinājums:
P vērtības aprēķināšanai izmantojiet šādus datus.

Šeit izlases lielums n = 200. Mums būs jāatrod izlases proporcija
= 128/200
 = 0,64
= 0,64
Z Statistika
Z statistikas aprēķins


= 0,64 - 0,60 / √ 0,60 * (1 - 0,60) / 200
Z statistika būs -

Z Statistika = 1,1547
P vērtība = P (z ≥ 1,1547)
Funkcija NORMSDIST programmā Excel

NORMSDIST būs -

NORMSDIST = 0,875893461
Pastāv iebūvēta funkcija, lai aprēķinātu p vērtību no Excel statistikas. Tā ir pazīstama kā funkcija NORMSDIST. Excel NORMSDIST funkcija aprēķina standarta parastā kumulatīvā izplatīšanas funkciju no piegādātās vērtības. Tās formāts ir NORMSDIST (z). Tā kā z statistikas vērtība ir šūnā B2, izmantotā funkcija ir = NORMSDIST (B2).
P vērtība būs -

P vērtība = 0,12410654
Tā kā mums jāatrod laukums pa labi no līknes,
p-vērtība = 1 - 0,875893 = 0,1224107
Tā kā p-vērtība 0.124107 ir vairāk nekā nozīmīgs 0.05 līmenis, mēs nespējam noraidīt nulles hipotēzi.
Atbilstība un izmantošana
P-Value ir plaši pielietojams statistisko hipotēžu testēšanā, īpaši nulles hipotēžu testēšanā. Piemēram, fonda pārvaldnieks vada kopfondu. Viņš apgalvo, ka atdeve no noteiktas kopfonda shēmas ir ekvivalenta Nifty, kas ir akciju tirgus indekss. Viņš pamatotu nulles hipotēzi, ka kopfondu shēmas ienesīgums ir līdzvērtīgs Nifty peļņai. Alternatīva hipotēze būtu tāda, ka shēmas ienesīgums un Nifty ienesīgums nav līdzvērtīgi. Pēc tam viņš aprēķinātu p vērtību.

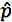 ir parauga proporcija
ir parauga proporcija