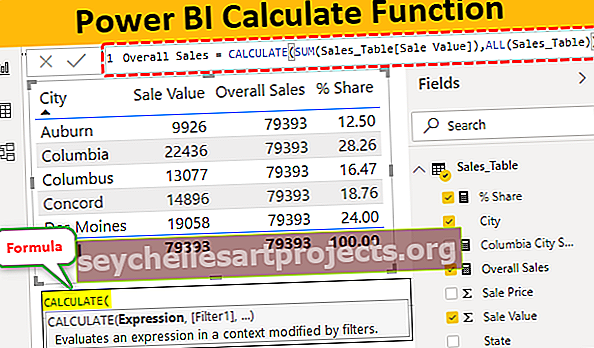
Parastā sadalījuma formula (pakāpeniski aprēķini)
Normāla izplatīšanas formula
Normālais sadalījums ir simetrisks sadalījums, ti, pozitīvās vērtības, un negatīvās izplatības vērtības var sadalīt vienādās pusēs, tāpēc vidējais, vidējais un režīms būs vienādi. Tam ir divas astes, viena ir pazīstama kā labā aste, bet otra - kreisā.
Aprēķina formulu var attēlot kā
X ~ N (µ, α)
Kur
- N = novērojumu skaits
- µ = novērojumu vidējais lielums
- α = standartnovirze
Lielākajā daļā gadījumu novērojumi neapstrādātajā veidā daudz neatklāj. Tāpēc ir ļoti svarīgi novērojumus standartizēt, lai varētu tos salīdzināt. Tas tiek darīts ar z-score formulas palīdzību. Novērošanai nepieciešams aprēķināt Z punktu skaitu.
Z rādītāja aprēķina vienādojums normālajam sadalījumam tiek parādīts šādi:
Z = (X-µ) / α
Kur
- Z = novērojumu Z-rezultāts
- µ = novērojumu vidējais lielums
- α = standartnovirze
Paskaidrojums
Sadalījums ir normāls, ja tas notiek pēc zvana līknes. Tas ir pazīstams kā zvana līkne, jo tas iegūst zvana formu. Viena no svarīgākajām normālās līknes īpašībām ir simetriska, kas nozīmē, ka pozitīvās un negatīvās vērtības sadalījumā var sadalīt vienādās pusēs. Vēl viena ļoti svarīga mainīgā būtnes īpašība ir tā, ka novērojumi būs 1 standarta novirzes robežās no vidējā 90% laika. Novērojumi būs divas standarta novirzes no vidējā 95% laika, un tas būs trīs standarta novirzēs no vidējā 99% laika.
Piemēri
Šo parasto izplatīšanas formulas Excel veidni varat lejupielādēt šeit - parastās izplatīšanas formulas Excel veidne1. piemērs
Skolēnu klases vidējais svars ir 65 kg, un svara standarts ir 5 kg. Ja pieņemam, ka atdeves sadalījums ir normāls, tad interpretēsim pēc klases skolēnu svara .
Ja sadalījums ir normāls, tad 68% no tā ir 1 standartnovirzes robežās, 95% - 2 standartnovirzēs un 99% - ar 3 standartnovirzēm.
Ņemot vērā
- Vidējā svara atdeve būs 65 kg
- Standarta novirze būs 3,5 kg

Tātad 68% gadījumu sadalījuma vērtība būs diapazonā, kā norādīts zemāk,

- Augšējais diapazons = 65 + 3,5 = 68,5
- Zemāks diapazons = 65-3,5 = 61,5
- Katra aste būs (68% / 2) = 34%
2. piemērs
Turpināsim ar to pašu piemēru. Skolēnu klases vidējais svars ir 65 kg, un svara standarts ir 3,5 kg. Ja mēs pieņemam, ka atdeves sadalījums ir normāls, tad interpretēsim to atbilstoši klases skolēnu svaram.
Ņemot vērā
- Vidējā svara atdeve būs 65 kg
- Standarta novirze būs 3,5 kg

Tātad 95% gadījumu sadalījuma vērtība būs diapazonā, kā norādīts zemāk,

- Augšējais diapazons = 65 + (3,5 * 2) = 72
- Zemākais diapazons = 65- (3,5 * 2) = 58
- Katra aste būs (95% / 2) = 47,5%
3. piemērs
Turpināsim ar to pašu piemēru. Skolēnu klases vidējais svars ir 65 kg, un svara standarts ir 3,5 kg. Ja mēs pieņemam, ka atdeves sadalījums ir normāls, tad interpretēsim to atbilstoši klases skolēnu svaram.
Ņemot vērā
- Vidējā svara atdeve būs 65 kg
- Standarta novirze būs 3,5 kg


Tātad 99% gadījumu sadalījuma vērtība būs diapazonā, kā norādīts zemāk,
- Augšējais diapazons = 65+ (3,5 * 3) = 75,5
- Zemākais diapazons = 65- (3,5 * 3) = 54,5
- Katra aste būs (99% / 2) = 49,5%
Atbilstība un izmantošana
Normālais sadalījums ir ļoti svarīgs statistikas jēdziens, jo lielākā daļa finanšu pasaules nejaušo mainīgo seko šādai līknei. Tam ir svarīga loma portfeļu veidošanā. Papildus finansēm tiek konstatēts, ka šāds sadalījums seko daudziem reālās dzīves parametriem. Piemēram, ja mēs mēģinām atrast studentu augstumu klasē vai studentu svaru klasē, novērojumi tiek sadalīti normāli. Tāpat arī eksāmena atzīmes seko tam pašam sadalījumam. Eksāmenā vērtējumu normalizēšana palīdz, ja lielākā daļa studentu ir sasnieguši zemākus vērtējumus, nosakot robežu, kurā teikts, ka tikai tie, kas neizdevās, ieguva zemāk par divām standarta novirzēm.