seychellesartprojects.org

Kas ir zvana līkne?

Zvana līkne ir normāls mainīgo lielumu varbūtības sadalījums, kas ir uzzīmēts uz grafika un ir kā zvana forma, kur līknes augstākais vai augšējais punkts ir visticamākais notikums no visiem sērijas datiem.

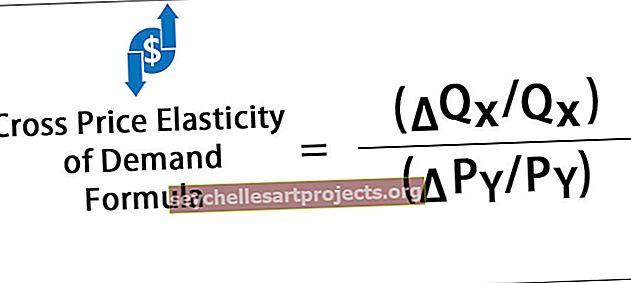
Zvana līknes formula, kā norādīts zemāk:

Kur,

• μ ir vidējais
• σ ir standartnovirze
• π ir 3,14159
• e ir 2,71828

Paskaidrojums

• Vidējo apzīmē ar μ, kas apzīmē sadalījuma centru vai viduspunktu.
• Horizontālā simetrija ap vertikālo līniju, kas ir x = μ, jo eksponentā ir kvadrāts.
• Standarta novirze tiek apzīmēta ar σ un ir saistīta ar sadalījuma izplatību. Palielinoties σ, normālais sadalījums izplatīsies vairāk. Konkrēti, izplatīšanas maksimums nav tik augsts, un sadalījuma aste kļūst biezāka.
• π ir konstante pi, un tam ir bezgalīgs skaitlis, kas neatkārto decimālo izplešanos.
• e apzīmē citu konstanti un ir arī pārpasaulīgs un iracionāls kā pi.
•  Eksponentā ir nepozitīva zīme, un pārējie termini ir kvadrāti eksponentā. Tas nozīmē, ka eksponents vienmēr būs negatīvs. Tāpēc šī funkcija palielina visu x vidējo μ vērtību.
• Vēl viena horizontāla asimptote atbilst horizontālajai līnijai y, kas ir vienāda ar 0, kas nozīmētu, ka funkcijas grafiks nekad neskars x asi un tam būs nulle.
• Kvadrātsakne Excel izteiksmē normalizēs formulu, kas nozīmē, ka, integrējot funkciju apgabala meklēšanai zem līknes, kur viss laukums būs zem līknes, un tas ir viens un tas atbilst 100%.
• Šī formula ir saistīta ar normālu sadalījumu un tiek izmantota varbūtību aprēķināšanai.

Piemēri

Šo Bell Curve Formula Excel veidni varat lejupielādēt šeit - Bell Curve Formula Excel veidne

1. piemērs

Apsveriet jums piešķirto vidējo vērtību, piemēram, 950, standartnovirze ir 200. Jums jāaprēķina y x = 850, izmantojot zvana līknes vienādojumu.

Risinājums:

Aprēķinam izmantojiet šādus datus

Pirmkārt, mums tiek dotas visas vērtības, ti, vidējā vērtība ir 950, standartnovirze kā 200 un x kā 850, mums vienkārši jāpievieno skaitļi formulā un jāmēģina aprēķināt y.

Zvana formas līknes formula, kā norādīts zemāk:

y = 1 / (200√2 * 3,14159) ^ e- (850–950) / 2 * (200 ^ 2)

y būs -

y = 0,0041

Pēc iepriekš minētās matemātikas veikšanas (pārbaudiet Excel veidni) y vērtība ir 0,0041.

2. piemērs

Sunita ir skrējēja un gatavojas gaidāmajām olimpiskajām spēlēm, un viņa vēlas noteikt, ka sacīkstēm, kuras viņa gatavojas vadīt, ir ideāls laika aprēķins, jo dalītā aizkavēšanās viņai var radīt zeltu olimpiskajās spēlēs. Viņas brālis ir statistiķis, un viņš atzīmēja, ka māsas vidējais laiks ir 10,33 sekundes, savukārt viņas laika vidējā novirze ir 0,57 sekundes, kas ir diezgan riskanti, jo šāda dalītā aizkavēšanās var likt viņai izcīnīt zeltu olimpiskajās spēlēs. Izmantojot zvana formas līknes vienādojumu, kāda ir varbūtība, ka Sunita sacensības veiks 10,22 sekundēs?

Risinājums:

Aprēķinam izmantojiet šādus datus

Pirmkārt, mums tiek piešķirtas visas vērtības, ti, vidējā vērtība ir 10,33 sekundes, standartnovirze - 0,57 sekundes un x - 10,22, mums vienkārši jāpievieno skaitļi formulā un jāmēģina aprēķināt y.

Zvana līknes formula, kā norādīts zemāk:

y = 1 / (0,57√2 * 3,14159) ^ e- (850–950) / 2 * (200 ^ 2)

y būs -

y = 0,7045

Pēc iepriekš minētās matemātikas veikšanas (pārbaudiet Excel veidni) y vērtība ir 0,7045.

3. piemērs

Hari-baktii limited ir revīzijas firma. Nesen tā ir saņēmusi ABC bankas obligāto revīziju, un viņi ir atzīmējuši, ka pēdējās revīzijās viņi ir izvēlējušies nepareizu paraugu, kas sniedza nepareizu informāciju par iedzīvotājiem, piemēram, debitoru parādsaistību gadījumā viņu atlasītais paraugs parāda, ka debitoru parāds ir īsts, bet vēlāk tika atklāts, ka debitoru populācijai bija daudz fiktīvu ierakstu.

Tāpēc tagad viņi mēģina analizēt, cik liela varbūtība ir iegūt slikto izlasi, kas populāciju vispārinātu kā pareizu, kaut arī izlase nebija pareiza šīs populācijas atainojums. Viņiem ir rakstu asistents, kurš labi pārvalda statistiku, un nesen viņš ir uzzinājis par zvana līknes vienādojumu.

Tātad, viņš nolemj izmantot šo formulu, lai atrastu varbūtību uzņemt vismaz 7 nepareizus paraugus. Viņš iegāja uzņēmuma vēsturē un atklāja, ka vidējais nepareizais paraugs, ko viņi savāc no populācijas, ir no 5 līdz 10 un standarta novirze ir 2.

Risinājums:

Aprēķinam izmantojiet šādus datus

Pirmkārt, mums jāņem 2 norādīto skaitļu vidējais lielums, ti, vidējais kā (5 + 10) / 2, kas ir 7,50, standartnovirze kā 2 un x kā 7, mums vienkārši jāpievieno skaitļi formulā un jāmēģina lai aprēķinātu y.

Zvana līknes formula, kā norādīts zemāk:

y = 1 / (2√2 * 3,14159) ^ e- (7 - 7,5) / 2 * (2 ^ 2)

y būs -

y = 0,2096

Pēc iepriekš minētās matemātikas veikšanas (pārbaudiet Excel veidni) y vērtība ir 0,2096

Tātad ir 21% iespēja, ka arī šoreiz viņi revīzijā varētu ņemt 7 nepareizus paraugus.

Atbilstība un lietojumi

Šo funkciju izmantos, lai aprakstītu fiziskus notikumus, ti, notikumu skaits ir ļoti liels. Vienkāršiem vārdiem sakot, iespējams, nevar prognozēt, kāds būs vienuma iznākums, ja ir vesela tonna novērojumu, bet jāspēj paredzēt, ko tie darīs kopumā. Veikt piemēru, pieņemsim, ka gāzes tvertnei ir nemainīga temperatūra, normālais sadalījums vai zvana līkne ļaus šai personai noskaidrot vienas daļiņas varbūtību, kas pārvietosies noteiktā ātrumā.

Finanšu analītiķis bieži izmantos parasto varbūtību sadalījumu vai teiks zvana līkni, analizējot tirgus vispārējās jutības vai drošības atdevi.

Piemēram, akcijas, kurām ir zvana līkne, parasti ir zilās mikroshēmas, un tām ir mazāks svārstīgums un bieži vien vairāk uzvedības modeļu, kas ir paredzami, un tāpēc tie izmanto akciju iepriekšējās peļņas normālo varbūtības sadalījumu vai zvana līkni, lai veiktu pieņēmumi par paredzamo atdevi.